
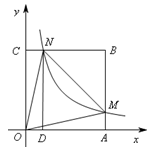
【题目】如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A.C分别在x轴、y轴上,反比例函数![]() 的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
①△OCN≌△OAM;
②ON=MN;
③四边形DAMN与△MON面积相等;
④若∠MON=450,MN=2,则点C的坐标为![]() .
.
其中正确的个数是( )
A.1 B.2 C.3 D.4
【答案】C.
【解析】
试题分析:设正方形OABC的边长为a,
则A(a,0),B(a,a),C(0,a),M(a,![]() ),N(
),N(![]() ,a).
,a).
∵CN=AM=![]() ,OC=OA= a,∠OCN=∠OAM=900,∴△OCN≌△OAM(SAS).结论①正确.
,OC=OA= a,∠OCN=∠OAM=900,∴△OCN≌△OAM(SAS).结论①正确.
根据勾股定理,![]() ,
,![]() ,∴ON和MN不一定相等.结论②错误.
,∴ON和MN不一定相等.结论②错误.
∵![]() ,∴
,∴![]() .结论③正确.
.结论③正确.
如图,过点O作OH⊥MN于点H,则
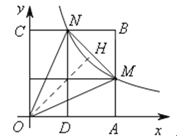
∵△OCN≌△OAM ,∴ON=OM,∠CON=∠AOM.
∵∠MON=450,MN=2,∴NH=HM=1,∠CON=∠NOH=∠HOM=∠AOM=22.50.
∴△OCN≌△OHN(ASA).∴CN=HN=1.∴![]() ,即
,即![]() .
.
由![]() ,得:
,得:![]() ,∴
,∴![]() ,∴
,∴![]() .
.
解得:![]() (舍去负值).
(舍去负值).
∴点C的坐标为![]() .结论④正确.∴结论正确的为①③④3个.故选C.
.结论④正确.∴结论正确的为①③④3个.故选C.


科目:初中数学 来源: 题型:
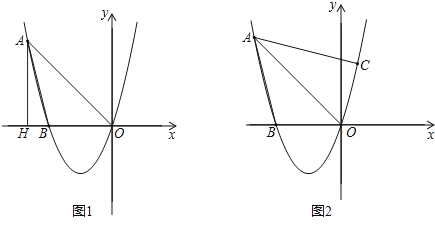
【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题.
例:若代数式![]() 的值是常数2,则a的取值范围 2≤a≤4 .
的值是常数2,则a的取值范围 2≤a≤4 .
分析:原式=|a﹣2|+|a﹣4|,而|a|表示数x在数轴上的点到原点的距离,|a﹣2|表示数a在数轴上的点到数2的点的距离,所以我们可以借助数轴进行分析.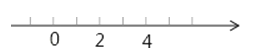
解:原式=|a﹣2|+|a﹣4|
在数轴上看,讨论a在数2表示的点左边;在数2表示的点和数4表示的点之间还是在数4表示的点右边,分析可得a的范围应是2≤a≤4.
(1)此例题的解答过程了用了哪些数学思想?请列举.
(2)化简![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
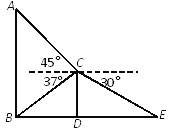
【题目】某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
(1)求建筑物CD的高度;
(2)求建筑物AB的高度.
(结果精确到0.1米,参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与x轴相交于点A(-2,0),与y轴交于点C,与反比例函数![]() 在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
(1)求一次函数的表达式;
(2)求反比例函数的表达式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com