
【题目】如图,□ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.
(1) 求证:△ADB≌△CEA;
(2) 若BD=6,求AF的长.
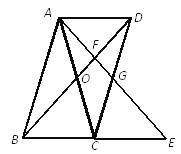
【答案】(1)△ADB≌△CEA;(2)2
【解析】试题分析:(1)由平行四边形的性质得出AD=BC,∠ABC+∠BAD=180°,由等腰三角形的性质得出∠ABC=∠ACB.证出∠BAD=∠ACE,CE=AD,由SAS证明△ADB≌△CEA即可;
(2)由全等三角形的性质得出AE=BD=6,由平行线得出△ADF∽△EBF,得出对应边成比例,即可得出结果.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠ABC+∠BAD=180°.
又∵AB=AC,
∴∠ABC=∠ACB.
∵∠ACB+∠ACE=180°,
∴∠BAD=∠ACE.
∵CE=BC,
∴CE=AD,
∴△ADB≌△CEA(SAS).
(2)解:∵△ADB≌△CEA,
∴AE=BD=6.
∵AD∥BC,
∴△ADF∽△EBF.
∴![]() .
.
∴![]() .
.
∴AF=2.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离;即
对应的点与原点的距离;即![]() ;这个结论可以推广为
;这个结论可以推广为![]() 表示在数轴上数
表示在数轴上数![]() ,
, ![]() 对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
对应点之间的距离.绝对值的几何意义在解题中有着广泛的应用:
例1:解方程![]() .
.
容易得出,在数轴上与原点距离为4的点对应的数为±4,即该方程的![]() ±4;
±4;
例2:解方程![]() .
.
由绝对值的几何意义可知,该方程表示求在数轴上与-1和2的距离之和为5的点对应的![]() 的值.在数轴上,-1和2的距离为3,满足方程的
的值.在数轴上,-1和2的距离为3,满足方程的![]() 对应的点在2的右边或在-1的左边.若
对应的点在2的右边或在-1的左边.若![]() 对应的
对应的
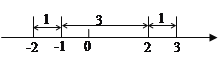
点在2的右边,如图可以看出![]() ;同理,若
;同理,若![]() 对应点在-1的左边,可得
对应点在-1的左边,可得![]() .所以原方程的解是
.所以原方程的解是![]() 或
或![]() .
.
例3:解不等式![]() .
.
在数轴上找出![]() 的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的
的解,即到1的距离为3的点对应的数为-2,4,如图,在-2的左边或在4的右边的![]() 值就满足
值就满足![]() ,所以
,所以![]() 的解为
的解为![]() 或
或![]() .
.
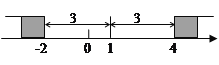
参考阅读材料,解答下列问题:
(1)方程![]() 的解为 ;
的解为 ;
(2)方程![]() 的解为 ;
的解为 ;
(3)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
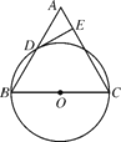
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com