
����Ŀ����ͼ, �ڶ�������ĺ�����MN����A��B���ۿڣ�������һ��С��P������ÿ�춼���ִ���A��B ���ۿ���AP��BP��·��ȥС��������ҵ����֪С��P��A�۵ı�ƫ��60��������B�۵ı�ƫ��45������С��P�ຣ����MN�ľ���Ϊ30����.
(1)��AP��BP�ij�(�ο����ݣ�![]() ��1.4��
��1.4��![]() ��1.7��
��1.7��![]() ��2.2)��
��2.2)��
(2)�ס��������ֱ��A��B���ۿ�ͬʱ����ȥС��P������ҵ���״����Ҵ�����С��24���ӣ���֪�״��ٶ����Ҵ��ٶȵ�1.2��������(1)�еĽ����ס����������ٶȸ��Ƕ��ٺ���/ʱ��

���𰸡���1��AP��60���BP��42(����)����2���״����ٶ���24����/ʱ���Ҵ����ٶ���20����/ʱ
��������
��1������P��PE��AB�ڵ�E������PE=30��������⣬��֪��PAB=30�㣬��PBA=45�����Ӷ��ɵ� AP��60�����Rt��PEB�У����ù��ɶ����������BP�ij���
(2)���Ҵ����ٶ���x����/ʱ����״����ٶ���1.2x����/ʱ�����ݼ״����Ҵ�����С��24�����г���ʽ���̣�������м��鼴�ɵ�.
(1)��ͼ������P��PE��MN������ΪE��
�����⣬�á�PAB��90�㣭60�㣽30�㣬��PBA��90�㣭45�㣽45�㣬
��PE��30�����AP��60���
��PE��MN����PBA��45�㣬���PBE����BPE�� 45�㣬
��PE��EB��30���
��Rt��PEB��BP��![]() ��30
��30![]() ��42���
��42���
��AP��60���BP��42(����)��

(2)���Ҵ����ٶ���x����/ʱ����״����ٶ���1.2x����/ʱ��
�������⣬��![]() ��
��
���x��20��
�����飬x��20��ԭ���̵Ľ⣬
�״����ٶ�Ϊ1.2x��1.2��20��24(����/ʱ).��
�𣺼״����ٶ���24����/ʱ���Ҵ����ٶ���20����/ʱ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD�У��Խ���AC��BD���ڵ�O���۵�������ֽƬABCD��ʹAD����BD�ϣ���Aǡ����BD�ϵĵ�F�غϣ�չ�����ۺ�DE�ֱ�AB��AC�ڵ�E��G������GF���������н��ۣ��١�ADG=22.5�㣻��tan��AED=2����S��AGD=S��OGD�����ı���AEFG�����Σ���BE=2OG������S��OGF=1����������ABCD�������6+4 ![]() ��������ȷ�Ľ��۸���Ϊ��������
��������ȷ�Ľ��۸���Ϊ�������� 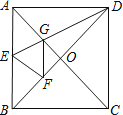
A.2
B.3
C.4
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±�Ϊij���꼾ˮ�����Ա��¼��ˮ��һ���ڵ�ˮλ�仯���������ˮλΪ150m������ĩ��ˮλ�պôﵽ����ˮλ����
���� | һ | �� | �� | �� | �� | �� | �� |
����/m | +1.2 | +0.4 | +0.8 | ��0.1 | +0.7 | ��0.7 | ��1.1 |
ע��������ʾ��ǰһ��ˮλ������������ʾ��ǰһ��ˮλ�½���
��1��������һ��ˮλ��ߣ��ж����ף�
��2��������һ��ˮλ��ͣ��ж����ף�
��3�����ݸ��������ݣ��Ծ���ˮλΪ0�㣬������ͳ��ͼ��ʾ�����ڸ�ˮ���ˮλ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ��
��1��3x-2=1-2��x+1��
��2��![]()
��3��2x+3��2x��1��=16-��x+1��
��4��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�����ô�μ����ƻ���400Ԫ����10��������Ʒ����ѡ������Ʒ���������±�����λ��Ԫ��
��ѡ������Ʒ | ���� | ���� | ��ë���� |
���ۣ�Ԫ�� | 50 | 40 | 25 |
��1����400Ԫȫ�����������������ë���Ĺ�10�������������ë���ĸ�������ټ���
��2����400Ԫȫ���������������������ë�������ֹ�10������ʵ���𣿣�����ʵ��ֱ��д��һ�ִ𰸼��ɣ���������˵������.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽������֪��ֽ������һ����(��ͼ��ʾ)��
![]()
����һ��
(1)�۵�ֽ�棬ʹ1��ʾ�ĵ��룭1��ʾ�ĵ��غϣ���3��ʾ�ĵ���________��ʾ�ĵ��غϣ�
��������
(2)�۵�ֽ�棬ʹ��1��ʾ�ĵ���3��ʾ�ĵ��غϣ��ش��������⣺
��5��ʾ�ĵ�����________��ʾ�ĵ��غϣ�
����������A��B����֮�����Ϊ11(A��B�����)����A��B���㾭�۵����غϣ���A��B�����ʾ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC ������BAC=90����AB=AC����D��BC��һ����������AD������A��AE��AD������ʼ�ձ���AE=AD������CE.
��1����֤����ABD ����ACE ��
��2����AFƽ����DAE��BC��F��̽���߶�BD��DF��FC֮���������ϵ����֤����
��3����(2)������������BD=3��CF=4����AD�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2��2ax+c��a��0�������ֵΪ4���������߹��㣨 ![]() ����
���� ![]() ������P��t��0����x���ϵĶ��㣬��������y�ύ��ΪC������ΪD��
������P��t��0����x���ϵĶ��㣬��������y�ύ��ΪC������ΪD��
��1����ö��κ����Ľ���ʽ��������D�����ꣻ
��2����|PC��PD|�����ֵ����Ӧ�ĵ�P�����ꣻ
��3����Q��0��2t����y���ϵĶ��㣬���߶�PQ�뺯��y=a|x|2��2a|x|+c��ͼ��ֻ��һ�������㣬��t��ȡֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�ƻ�����һ��������Ϊ���˽�ѧ���Կ����������������ѧУ������һ�Ρ�����ϲ���Ŀ������ĵ��飬�����ˡ���ѧ���������ա������������͡��������ĸ���𣬹涨ÿ�˱��벢��ֻ��ѡ������һ�࣬�ִ�ȫ��ѧ���ĵ�����������ȡ�˲���ѧ���ĵ��������ͳ�ƣ�����ͳ�ƽ����������ͼ��ʾ��������������ͳ��ͼ����������ͳ��ͼ�У�����������������ε�Բ�Ľ����ȣ�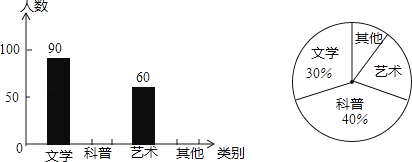
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com