
����Ŀ����ͼ1��������OABC�ı�OA�������ϣ�OΪԭ�㣬������OABC�����Ϊ12��OC�߳�Ϊ3.

(1)�����ϵ�A��ʾ����Ϊ________��
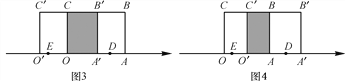
(2)��������OABC������ˮƽ�ƶ����ƶ���ij����μ�ΪO��A��B��C�����ƶ���ij�����O��A��B��C����ԭ������OABC�ص�����(��ͼ2����Ӱ����)�������ΪS.
�ٵ�Sǡ�õ���ԭ������OABC�����һ��ʱ�������ϵ�A����ʾ�����Ƕ��٣�
�� �����A���ƶ�����AA����x.
�� ����)��S��4ʱ����x��ֵ��
�� ����)DΪ�߶�AA�����е㣬��E���߶�OO���ϣ���OE��![]() OO��������D��E����ʾ������Ϊ�෴��ʱ����x��ֵ��
OO��������D��E����ʾ������Ϊ�෴��ʱ����x��ֵ��
���𰸡�4
����������1���������+OC�ɵ�AO�������ɵô𰸣�
��2�������ȼ����S��ֵ���ٸ��ݾ��ε������ʾ��O/A�ij��ȣ��ٷ�����������������˶�ʱ�������˶�ʱ���ֱ����A/��ʾ������
��i�����ȸ�������ɵ�OA/�ij��ȣ�����OA����ȥOA/���ɵ�x��ֵ��
Ii������������������ԭ������OABC�����ƶ�ʱ����D��ʾ����Ϊ4 -![]() x����E��ʾ����Ϊ-
x����E��ʾ����Ϊ-![]() x��ԭ������OABC�����ƶ�ʱ����D��E��ʾ������������������������.
x��ԭ������OABC�����ƶ�ʱ����D��E��ʾ������������������������.
�⣺��1���߳�����OABC�����Ϊ12��OC�߳�Ϊ3��
��OA=12��3=4��
�������ϵ�A��ʾ����Ϊ4.
�ʴ�Ϊ��4.
(2)����ΪSǡ�õ���ԭ������OABC�����һ�룬����S��6������O��A��6��3��2����������OABC�����˶�ʱ����ͼ3��A����ʾ����Ϊ2����������OABC�����˶�ʱ����ͼ4����ΪO��A����AO��4������OA����4��4��2��6������A����ʾ����Ϊ6.�������ϵ�A����ʾ������6��2.
 ��
��
�ڣ�i)��ͼ3���������CO��OA����4����ΪCO��3������OA����![]() ������x��4��
������x��4��![]() ��
��![]()
��ii)��ͼ3����ԭ������OABC�����ƶ�ʱ����D��ʾ����Ϊ4��![]() x����E��ʾ����Ϊ��
x����E��ʾ����Ϊ��![]() x��������ɵ÷��̣�4��
x��������ɵ÷��̣�4��![]() x��
x��![]() x��0�����x��
x��0�����x��![]() ����ͼ4����ԭ������OABC�����ƶ�ʱ����D��E��ʾ�����������������������⣬����ȥ��������������x��
����ͼ4����ԭ������OABC�����ƶ�ʱ����D��E��ʾ�����������������������⣬����ȥ��������������x��![]() .
.
���㾦��������Ҫ������һԪһ�η��̵�Ӧ�ã����ᣬ����ؼ�����ȷ�������⣬�������ν���г����̣�ע��Ҫ�������ۣ���Ҫ©��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B��C��ͬһ�������ϣ����е�A��B��ʾ�����ֱ�Ϊ��3��1����BC=2����AC���ڣ�������
A.3
B.2
C.3��5
D.2��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
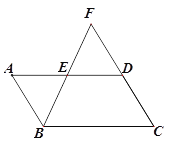
����Ŀ����ͼ����ABCD�У�EΪAD���е㣬BE��CD�ཻ�ڵ�F.
��1����֤��AB=DF
��2������DEF�����ΪS1����BCF�����ΪS2����S12-S2+4=0�����ABCD�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijҩƷ�������ν��ۣ�ÿƿ���ۼ���168Ԫ��Ϊ108Ԫ����֪���ν��۵İٷ�����ͬ����ÿ�ν��۵İٷ���Ϊx�����������з��̵ã�������
A.168��1+x��2��108B.168��1��x��2��108
C.168��1��2x����108D.168y��x2��1��x2����108
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧҪ����A��C���صľ��룬��A��C֮����һˮ�أ�����ֱ�Ӳ�������������A��Cͬһˮƽ����ѡȡ��һ��B����B��ֱ�ӵ���A��C���أ��������õ�AB=80�ף�BC=20�ף���ABC=120�㣮�������С��ͬѧ���A��C����֮��ľ��룮���ο����� ![]() ��4.6��
��4.6�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��B�������Ϸֱ��ʾ������a��b����A��ԭ��O����֮��� �����ʾΪAO����AO��|a-0|��|a|�����Ƶأ���B��ԭ��O����֮��ľ����ʾ ΪBO����BO��|b|����A���B����֮��ľ����ʾΪAB��|a-b|.�������ᣬ˼�����ش��������⣺
(1)�������ϱ�ʾ1�ͣ�3������֮��ľ�����__________��
�������ϱ�ʾm�ͣ�1������֮��ľ�����__________��
�������ϱ�ʾm�ͣ�1������֮��ľ�����3����������m��___________��
(2)��x��ʾһ��������������x�ȣ�3��x��1С����|x-1|+|x+3|=______��
(3)������|x-2|+|x+4|=6����������x�ĺ�.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ�������ϣ����ɸ���ȫ��ͬ���ⳤΪ10cm��С������ѳ�һ�������壮
��1�������������______�����������.
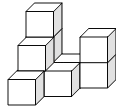
��2�������������л�������ͼ����ͼ.
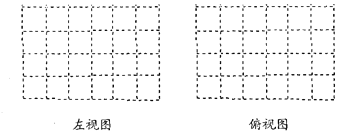
��3����������������ı��棨�������棩���ϻ�ɫ���ᣬ��������������������Ƕ���cm2.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ƽ�������֣���ԲΪͬһ��ļ������ǣ� ��
A.��
B.����
C.Բ
D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���� �� ��
A. ����3��������5��=��8B. ����3��������5��=��8
C. ����3��3=��9D. ��32=��9
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com