
【题目】如图,在ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 . 
【答案】24
【解析】解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,
∴∠DAB+∠CBA=180°,
又∵AP和BP分别平分∠DAB和∠CBA,
∴∠PAB+∠PBA= ![]() (∠DAB+∠CBA)=90°,
(∠DAB+∠CBA)=90°,
在△APB中,∠APB=180°﹣(∠PAB+∠PBA)=90°;
∵AP平分∠DAB,
∴∠DAP=∠PAB,
∵AB∥CD,
∴∠PAB=∠DPA
∴∠DAP=∠DPA
∴△ADP是等腰三角形,
∴AD=DP=5,
同理:PC=CB=5,
即AB=DC=DP+PC=10,
在Rt△APB中,AB=10,AP=8,
∴BP= ![]() =6,
=6,
∴△APB的周长=6+8+10=24;
所以答案是:24.
【考点精析】根据题目的已知条件,利用平行线的性质和三角形的内角和外角的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
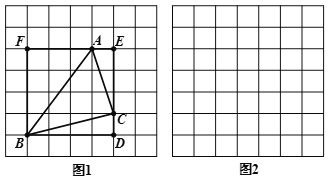
【题目】莫小贝在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC 的面积.
(1)莫小贝所画的△ABC 的三边长分别是AB=_______,BC=______,AC=______;△ABC 的面积为________.
(2)已知△ABC 中,AB=![]() ,BC=
,BC=![]() ,AC=
,AC=![]() ,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现与探索.
(1)根据小明的解答(图1)将下列各式因式分解

①a2-12a+20
②(a-1)2-8(a-1)+7
③a2-6ab+5b2
(2)根据小丽的思考(图2)解决下列问题.
①说明:代数式a2-12a+20的最小值为-16.
②请仿照小丽的思考解释代数式-(a+1)2+8的最大值为8,并求代数式-a2+12a-8的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y= ![]() (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0). 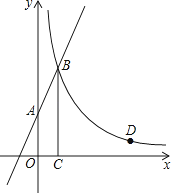
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y= ![]() (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
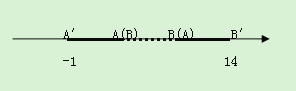
【题目】(1)如图,在数轴上有一小木棒AB,若平移木棒,使B落在A处,则A′所表示的数为 -1,若将A落在B处时,则B′所表示的数14,它的两个端点A、B所表示的数分别是 、 .
(2)老师给东东出了一道关于年龄的数学题:我像你那么小时,你才两岁;你像我那么大时,我已经44岁了,你猜我有多少岁?亲爱的同学,你能不能利用上一题的方法帮助小东求出老师的年龄呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,过点
,过点![]() ,
,![]() 作
作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
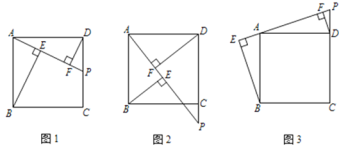
,![]() ,如图1.
,如图1.
(1)请探究![]() ,
,![]() ,
,![]() 这三条线段有怎样的数量关系?请说明理由;
这三条线段有怎样的数量关系?请说明理由;
(2)若点![]() 在
在![]() 的延长线上,如图2,那么这三条线段的数量关系是 (直接写结果)
的延长线上,如图2,那么这三条线段的数量关系是 (直接写结果)
(3)若点![]() 在
在![]() 的延长线上,如图3,那么这三条线段的数量关系是 (直接写结果)
的延长线上,如图3,那么这三条线段的数量关系是 (直接写结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com