
【题目】已知,点P是等边△ABC内一点,PA=4,PB=3,PC=5.线段AP绕点A逆时针旋转60°到AQ,连接PQ.(1)求PQ的长。(2)求∠APB的度数。
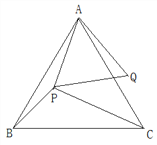
【答案】(1)4(2)150°
【解析】试题分析:(1)由旋转的性质可知AP=AQ,然后可证明△APQ为等边三角形,从而可求得PQ的长;
(2)先依据等边三角形的性质证明△APB≌△AQC,从而得到QC的长,然后依据勾股定理的逆定理证明△PQC为直角三角形,故此可求得∠AQC的度数,从而得到∠APB的度数.
解:(1)∵AP=AQ,∠PAQ=60°
∴△APQ是等边三角形,
∴PQ=AP=4.
(2)连接QC.
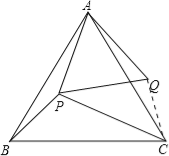
∵△ABC、△APQ是等边三角形,
∴∠BAC=∠PAQ=60°,
∴∠BAP=∠CAQ=60°﹣∠PAC.
在△ABP和△ACQ中![]() ,
,
∴△ABP≌△ACQ.
∴BP=CQ=3,∠APB=∠AQC,
∵在△PQC中,PQ2+CQ2=PC2
∴△PQC是直角三角形,且∠PQC=90°
∵△APQ是等边三角形,
∴∠AQP=60°
∴∠APB=∠AQC=60°+90°=150°.


科目:初中数学 来源: 题型:
【题目】已知点P(a,a+3)在抛物线y=x2﹣7x+19图象上,则点P关于原点O的对称点P′的坐标是( )
A.(4,7)
B.(﹣4,﹣7)
C.(4,﹣7)
D.(﹣4,7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织师生开展植树造林活动,为了了解全校4000名学生的情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整)。

(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的平均数;
(3)根据抽样数据,估计该校4000名学生的植树数量。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm B.7cm,4cm,2cm
C.3cm,4cm,8cm D.3cm,3cm,4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. 3a2+a=4a3 B. -2(a-b)=-2a+ b C. 5a-4a=1 D. a2b-2a2 b =-a2 b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com