【题目】学校组织师生开展植树造林活动，为了了解全校4000名学生的情况，随机抽样调查50名学生的植树情况，制成如下统计表和条形统计图（均不完整）。
（1）将统计表和条形统计图补充完整；
（2）求抽样的50名学生植树数量的平均数；
（3）根据抽样数据，估计该校4000名学生的植树数量。
【答案】(1)答案见解析；（2）4.6棵；（3）18400棵.
【解析】
试题分析：（1）用总人数减去其他小组的人数即可求得植树棵树为5的小组的频数，除以总人数即可得到该组的频率；
（2）用加权平均数计算植树量的平均数即可；
（3）用样本的平均数估计总体的平均数即可．
试题解析：1）统计表和条形统计图补充如下：
植树量为5棵的人数为：50-5-20-10=15，频率为：15÷50=0.3，，
（2）抽样的50名学生植树的平均数是：
=4.6（棵）．
（3）∵样本数据的平均数是4.6，
∴估计该校4000名学生参加这次植树活动的总体平均数是4.6棵．
于是4.6×4000=18400（棵），
∴估计该校800名学生植树约为18400棵．
学练快车道快乐假期寒假作业系列答案科目：初中数学 来源： 题型：
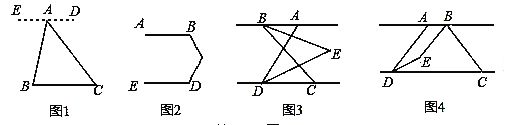
【题目】 阅读并补充下面推理过程：（1）
如图1，已知点A是BC外一点，连接AB，AC．
求∠BAC+∠B+∠C的度数．
解：过点A作ED∥BC，所以∠B= ，∠C= ．
又因为∠EAB+∠BAC+∠DAC=180°．
所以∠B+∠BAC+∠C=180°．
方法运用：（2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数．
深化拓展：（3）已知AB∥CD，点C在点D的右侧，∠ADC=70°，BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间．
．如图3，点B在点A的左侧，若∠ABC=60°，则∠BED的度数为 °．
Ⅱ．如图4，点B在点A的右侧，且AB＜CD，AD＜BC．若∠ABC=n°，则∠BED的度数为 °．（用含n的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图所示，△ABC为任意三角形，若将△ABC绕点C顺时针旋转180°得到△DEC。
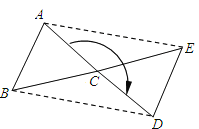
(1)试猜想AE与BD有何关系？说明理由；
(2)请给△ABC添加一个条件，使旋转得到的四边形ABDE为矩形，并说明理由
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了解某种电动汽车的性能，对这种电动汽车进行了抽检，将一次充电后行驶的里程数分为A，B，C，D四个等级，其中相应等级的里程依次为200千米，210千米，220千米，230千米，获得如下不完整的统计图．
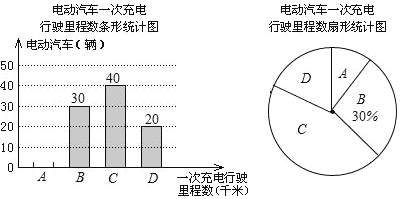
根据以上信息，解答下列问题：
（1）问这次被抽检的电动汽车共有几辆？并补全条形统计图；
（2）估计这种电动汽车一次充电后行驶的平均里程数为多少千米？
查看答案和解析>>
科目：初中数学 来源： 题型：
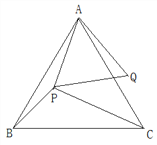
【题目】已知，点P是等边△ABC内一点，PA=4,PB=3,PC=5.线段AP绕点A逆时针旋转60°到AQ,连接PQ.(1)求PQ的长。（2）求∠APB的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com