
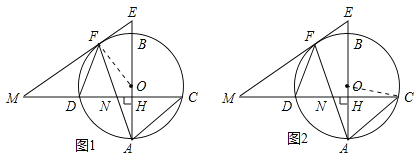
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=![]() ,AN=
,AN=![]() ,求圆O的直径的长度.
,求圆O的直径的长度.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OF,根据切线的性质结合四边形内角和为360°,即可得出∠M+∠FOH=180°,由三角形外角结合平行线的性质即可得出∠M=∠C=2∠OAF,再通过互余利用角的计算即可得出∠CAN=90°﹣∠OAF=∠ANC,由此即可证出CA=CN;
(2)连接OC,由圆周角定理结合cos∠DFA=![]() ,AN=
,AN=![]() ,即可求出CH、AH的长度,设圆的半径为r,则OH=r﹣6,根据勾股定理即可得出关于r的一元一次方程,解之即可得出r,再乘以2即可求出圆O直径的长度.
,即可求出CH、AH的长度,设圆的半径为r,则OH=r﹣6,根据勾股定理即可得出关于r的一元一次方程,解之即可得出r,再乘以2即可求出圆O直径的长度.
试题解析:(1)证明:连接OF,则∠OAF=∠OFA,如图所示.
∵ME与⊙O相切,∴OF⊥ME.∵CD⊥AB,∴∠M+∠FOH=180°.
∵∠BOF=∠OAF+∠OFA=2∠OAF,∠FOH+∠BOF=180°,∴∠M=2∠OAF.
∵ME∥AC,∴∠M=∠C=2∠OAF.
∵CD⊥AB,∴∠ANC+∠OAF=∠BAC+∠C=90°,∴∠ANC=90°﹣∠OAF,∠BAC=90°﹣∠C=90°﹣2∠OAF,∴∠CAN=∠OAF+∠BAC=90°﹣∠OAF=∠ANC,∴CA=CN.
(2)连接OC,如图2所示.
∵cos∠DFA=![]() ,∠DFA=∠ACH,∴
,∠DFA=∠ACH,∴![]() =
=![]() .设CH=4a,则AC=5a,AH=3a,∵CA=CN,∴NH=a,∴AN=
.设CH=4a,则AC=5a,AH=3a,∵CA=CN,∴NH=a,∴AN=![]() =
=![]() =
=![]() a=
a=![]() ,∴a=2,AH=3a=6,CH=4a=8.
,∴a=2,AH=3a=6,CH=4a=8.
设圆的半径为r,则OH=r﹣6,在Rt△OCH中,OC=r,CH=8,OH=r﹣6,∴OC2=CH2+OH2,r2=82+(r﹣6)2,解得:r=![]() ,∴圆O的直径的长度为2r=
,∴圆O的直径的长度为2r=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学了解本校学生对球类运动的爱好情况,分为足球、篮球、排球、其他四个方面调查若干名学生,每人只选其中之一,统计后绘制成不完整的“折线统计图”(扇形统计图),根据信息解答下列问题: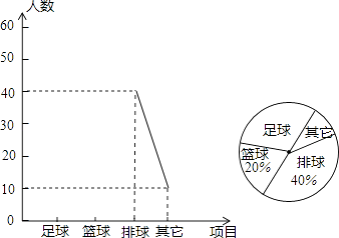
(1)在这次调查中,一共调查名学生;
(2)在扇形统计图中,“足球”所在扇形圆心角度;
(3)将折线统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】P(x,y)在第三象限,且到y 轴距离为3,到x 轴距离为5,则P点的坐标是( )
A. (-3,-5) B. (5,-3) C. (3,-5) D. (-3,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
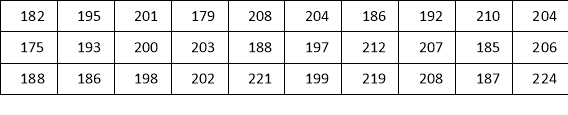
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
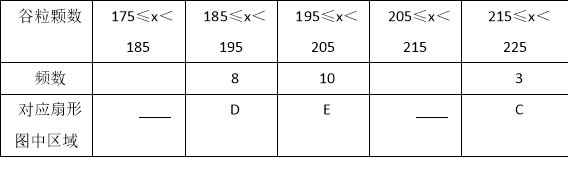
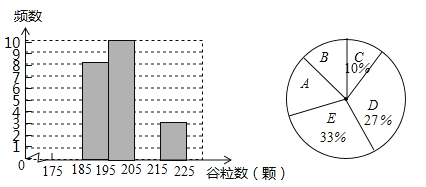
如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数![]() (a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为
(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为![]() ,直线l的解析式为y=x.
,直线l的解析式为y=x.
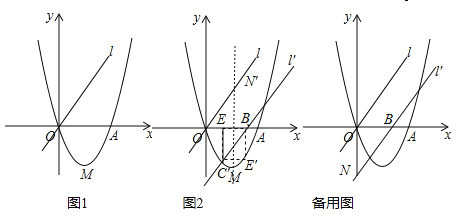
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上林老师出示了问题:如图,AD∥BC,∠AEF=90°AD=AB=BC=DC,∠B=90°,点E是边BC的中点,且EF交∠DCG的平分线CF于点F,求证:AE=EF.
同学们作了一步又一步的研究: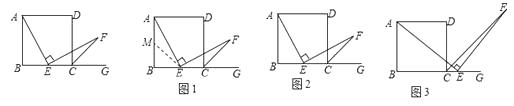
(1)、经过思考,小明展示了一种解题思路:如图1,取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF,小明的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)、小颖提出一个新的想法:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)、小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com