
【题目】数学课上林老师出示了问题:如图,AD∥BC,∠AEF=90°AD=AB=BC=DC,∠B=90°,点E是边BC的中点,且EF交∠DCG的平分线CF于点F,求证:AE=EF.
同学们作了一步又一步的研究: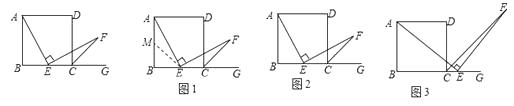
(1)、经过思考,小明展示了一种解题思路:如图1,取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF,小明的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)、小颖提出一个新的想法:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)、小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
【答案】
(1)解:正确.
∵M是AB的中点,E是BC的中点 AB=BC
∴AM=EC BM=BE
∴∠BME=45°
∠AME=135°
∵CF是∠DCG的平分线
∴∠DCF=45°
∠ECF=135°
∴∠AME=∠ECF
∵∠AEB+∠BAE=90°
∠AEB+∠CEF=90°
∴∠BAE=∠CEF
∴△AME≌△BCF(ASA)
∴AE=EF
(2)解:正确.
在AB上取一点M,使AM=BC,连接ME.
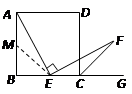
∴BM=BE ∴∠BME=45°∴∠AME=135°,
∵CF是∠DCG的平分线 ∴∠DCF=45° ∠ECF=135°
∴∠AME=∠ECF
∵∠AEB+∠BAE=90° ∠AEB+∠CEF=90°
∴∠BAE=∠CEF
∴△AME≌△BCF(ASA) ∴AE=EF
(3)解:正确.
在BA的延长线上取一点N.使AN=CE,连接NE.
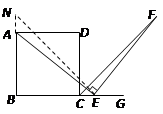
∴BN=BE ∠N=∠PCE=45°
∵AD∥BE ∴∠DAE=∠BAE ∴∠NAE=∠CEF ∴△ANE≌△ECF(ASA) ∴AE=EF
【解析】(1)取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,从而证出AE=EF;
(2)在AB上取一点M,使AM=BC,连接ME.再证明△AME≌△ECF,从而证出AE=EF;
(3)在BA的延长线上取一点N.使AN=CE,连接NE.证法与②同.


科目:初中数学 来源: 题型:
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA=![]() ,AN=
,AN=![]() ,求圆O的直径的长度.
,求圆O的直径的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AB+AC=2AE中正确的是.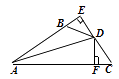
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次射击比赛中,甲、乙两名运动员10次射击的平均成绩都是7环,其中甲的成绩的方差S甲2=1.21,乙的成绩的方差S乙2=3.98,由此可知( ).
A. 甲比乙的成绩稳定 B. 乙比甲的成绩稳定
C. 甲、乙两人的成绩一样稳定 D. 无法确定谁的成绩更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
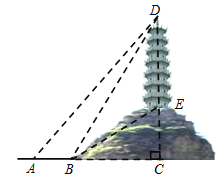
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决老百姓看病贵的问题,对某种原价为400元的药品进行连续两次降价,降价后的价格为256元,设每次降价的百分率为x,则依题意列方程为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com