
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
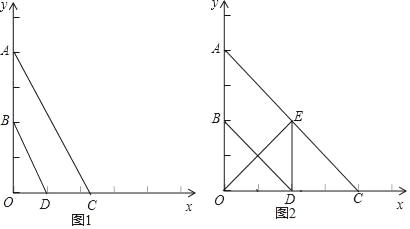
【题目】如图,已知直线 y=![]() x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
(1)当 x =______________时,PB+PC 的值最小;
(2)当 x =______________时,|PB-PC|的值最大.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.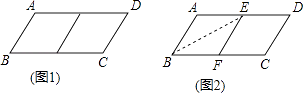
(1)判断与推理:
①邻边长分别为2和3的平行四边形是阶准菱形;
(2)小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABFE是菱形.
(3)操作、探究与计算:
①已知ABCD的邻边长分别为1,a(a>1),且是3阶准菱形,请画出ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出ABCD是几阶准菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差是一个常数,这个常数是 ;根据此规律,如果![]() (
(![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() ,
,![]() ;
;
②如果欲求![]() 的值,可令
的值,可令
![]() ……………①
……………①
将①式右边顺序倒置,得![]() ……………②
……………②
由②加上①式,得2![]() ;
;
∴ S=_________________;
由结论求![]() ;
;
(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ;根据此规律,如果![]() (
(![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() ,
,![]() ;
;
②为了求![]() 的值,可令
的值,可令![]() ,则
,则![]() ,因此
,因此![]() ,所以
,所以![]() ,
,
即![]() .
.
仿照以上推理,计算![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘西自治州风景优美,物产丰富,一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产.若购买3盒豆腐乳和2盒猕猴桃果汁共需180元;购买1盒豆腐乳和3盒猕猴桃果汁共需165元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )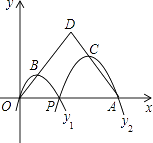
A.![]()
B.![]()
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某品牌A,B两种型号冰箱的销售情况,王明对某专卖店一到七月份的销售情况进行了统计,并将得到的数据制成如下统计表:
月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
A型销 售量(台) | 10 | 14 | 17 | 16 | 13 | 14 | 14 |
B型销 售量(台) | 6 | 10 | 14 | 15 | 16 | 17 | 20 |
完成下表:
平均数(台) | 中位数(台) | 方差 | |
A型销售量 | 14 | ||
B型销售量 | 14 | 18.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是市民广场到解百地下通道的手扶电梯示意图.其中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是 ![]() m,则乘电梯从点B到点C上升的高度h是 m.
m,则乘电梯从点B到点C上升的高度h是 m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com