
【题目】如图,已知直线 y=![]() x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
(1)当 x =______________时,PB+PC 的值最小;
(2)当 x =______________时,|PB-PC|的值最大.

【答案】 3 -21
【解析】试题分析:(1)作点B关于x轴的对称点点B',连接B'C交x轴与点P,此时PB+PC 的值最小,作CD⊥x轴交于点D,要求点P的横坐标即要求直线B'C的解析式,即要求点B'、C的坐标,B'坐标不难求,C的坐标通过△AOB≌△CDA全等可以求得;(2)延长CB交x轴于点P,此时|PB-PC|的值最大,要求点P横坐标,即要求直线BC的解析式,求出直线BC的解析式,令y=0,求出点P的坐标即可.
试题解析:
(1)作点B关于x轴的对称点点B',连接B'C交x轴与点P,此时PB+PC 的值最小,作CD⊥x轴交于点D,
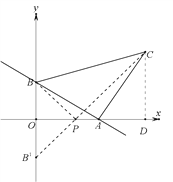
令x=0,y=3,B(0,3);令y=0,x=4,A(4,0),
∴B'(0,-3),AO=4,BO=3,
∵等腰Rt△ABC,∴∠BAC=90°,AB=AC,
∴∠BAO+∠CAD=90°,
∵∠CAD+∠ACD=90°,
∴∠BAO=∠ACD,
在△AOB和△CDA中,
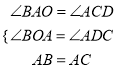 ,
,
∴△AOB≌△CDA,
∴AO=CD=4,BO=AD=3,
∴OD=7,
∴C(7, 4),
设直线B'C的解析式为:y=kx+b,
![]() ,解得
,解得![]() ,
,
∴y=x-3,
令y=0,x=3;
(2)延长CB交x轴于点P,此时|PB-PC|的值最大,
设直线BC解析式为:y=kx+b,
![]() ,解得
,解得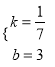 ,
,
∴y=![]() x+3,
x+3,
令y=0,x=-21.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:
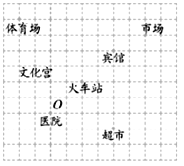
【题目】如图,这是某市部分简图,为了确定各建筑物的位置请完成以下步骤.
(1)请你以火车站为原点建立平面直角坐标系;
(2)写出市场的坐标是____________;超市的坐标为____________;
(3)请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,画出平移后的△A1B1C1,并求出其面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知点A、点B是直线上的两点,AB =12厘米,点C在线段AB上,且AC=8厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发,在直线上运动,则经过 秒时线段PQ的长为5厘米.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,山坡斜面CD与水平面夹角为30°,坡面上点E处有一亭子,测得假山坡脚C与楼房水平距离BC=10米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.求楼房AB的高(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.
(1)求降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠DFB=![]() ∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的结论是_______.
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的结论是_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com