
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1) (1)A(2,0);C(0,4);(2) 直线CD解析式为y=-![]() x+4.(3)P1(0,0);P2(
x+4.(3)P1(0,0);P2(![]() ,
,![]() );P3(-
);P3(-![]() ,
,![]() ).
).
【解析】
试题分析:(1)已知直线y=-2x+4与x轴、y轴分别交于点A、C,即可求得A和C的坐标;
(2)根据题意可知△ACD是等腰三角形,算出AD长即可求得D点坐标,最后即可求出CD的解析式;
(3)将点P在不同象限进行分类,根据全等三角形的判定方法找出所有全等三角形,找出符合题意的点P的坐标.
试题解析:(1)A(2,0);C(0,4)
(2)由折叠知:CD=AD.设AD=x,则CD=x,BD=4-x,
根据题意得:(4-x)2+22=x2解得:x=![]()
此时,AD=![]() ,D(2,
,D(2,![]() )
)
设直线CD为y=kx+4,把D(2,![]() )代入得
)代入得![]() =2k+4
=2k+4
解得:k=-![]()
∴该直线CD解析式为y=-![]() x+4.
x+4.
(3)①当点P与点O重合时,△APC≌△CBA,此时P(0,0)
②当点P在第一象限时,如图,
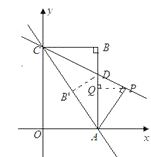
由△APC≌△CBA得∠ACP=∠CAB,
则点P在直线CD上.过P作PQ⊥AD于点Q,
在Rt△ADP中,
AD=![]() ,PD=BD=4-
,PD=BD=4-![]() =
=![]() ,AP=BC=2
,AP=BC=2
由AD×PQ=DP×AP得:![]() PQ=3
PQ=3
∴PQ=![]()
∴xP=2+![]() =
=![]() ,
,
把x=![]() 代入y=-
代入y=-![]() x+4得y=
x+4得y=![]()
此时P(![]() ,
,![]() )
)
(也可通过Rt△APQ勾股定理求AQ长得到点P的纵坐标)
③当点P在第二象限时,如图
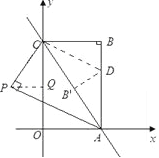
同理可求得:CQ=![]()
∴OQ=4-![]() =
=![]()
此时P(-![]() ,
,![]() )
)
综合得,满足条件的点P有三个,
分别为:P1(0,0);P2(![]() ,
,![]() );P3(-
);P3(-![]() ,
,![]() ).
).


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】如图①,将笔记本活页一角折过去,使角的顶点A落在![]() 处,BC为折痕。
处,BC为折痕。
(1)图①中,若∠1=30°,求∠![]() 的度数;
的度数;
(2)如果又将活页的另一角斜折过去,使BD边与BA重合,折痕为BE,如图②所示,∠1=30°,求∠2以及∠![]() 的度数;
的度数;
(3)如果在图②中改变∠1的大小,则![]() 的位置也随之改变,那么问题(2)中∠
的位置也随之改变,那么问题(2)中∠![]() 的大小是否改变?请说明理由。
的大小是否改变?请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某房地产开发公司计划建![]() 、
、![]() 两种户型的住房共80套,该公司所筹资金不少于
两种户型的住房共80套,该公司所筹资金不少于![]() 万元,但不超过
万元,但不超过![]() 万元,且所筹资金全部用于建房,两种户型的建房的成本和售价如表:
万元,且所筹资金全部用于建房,两种户型的建房的成本和售价如表:
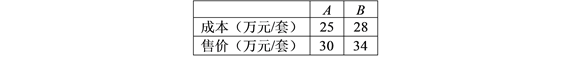
(![]() )该公司对这两种户型住房有哪几种方案?
)该公司对这两种户型住房有哪几种方案?
(![]() )该公司如何建房获利利润最大?
)该公司如何建房获利利润最大?
(![]() )根据市场调查,每套
)根据市场调查,每套![]() 型住房的售价不会改变,每套
型住房的售价不会改变,每套![]() 型住房的售价将会提高
型住房的售价将会提高![]() 万元
万元![]() ,且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?
,且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线 y=![]() x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
(1)当 x =______________时,PB+PC 的值最小;
(2)当 x =______________时,|PB-PC|的值最大.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上表示整数的点称为整点,某数轴的单位长度为1cm,若在数轴上画出一条长2019cm的线段AB,则AB盖住的整点个数是( )
A.2019或2020B.2018或2019C.2019D.2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差( | |
初中部 | a | 85 | b |
|
高中部 | 85 | c | 100 | 160 |
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差![]() ,并判断哪一个代表队选手成绩较为稳定.
,并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校原有600张旧课桌急需维修,经过A、B、C三个工程队的竞标得知,A、B的工作效率相同,且都为C队的2倍,若由一个工程队单独完成,C队比A队要多用10天.学校决定由三个工程队一齐施工,要求至多6天完成维修任务.三个工程队都按原来的工作效率施工2天时,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,A、B队提高的工作效率仍然都是C队提高的2倍.这样他们至少还需要3天才能完成整个维修任务.
(1)求工程队A原来平均每天维修课桌的张数;
(2)求工程队A提高工作效率后平均每天多维修课桌张数的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,码头A、B分别在海岛O的北偏东45°和北偏东60°方向上,仓库C在海岛O的北偏东75°方向上,码头A、B均在仓库C的正西方向,码头B和仓库C的距离BC=50km,若将一批物资从仓库C用汽车运送到A、B两个码头中的一处,再用货船运送到海岛O,若汽车的行驶速度为50km/h,货船航行的速度为25km/h,问这批物资在哪个码头装船,最早运抵海岛O?(两个码头物资装船所用的时间相同,参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com