
【题目】如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.

【答案】(1)①∠AOD=120°;②猜想∠BOC+∠AOD=180°,证明见解析;(2)120°.
【解析】试题分析:(1)①根据直角的定义先求出∠AOB,再根据角的和差关系即可得出答案;
②得到∠AOD+∠BOC=∠BOD+∠AOC,代入求出即可;
(2)类比②可得:∠AOD+∠BOC=∠BOD+∠AOC,依此代入计算即可求解.
试题解析:
(1)①∵∠AOC和∠BOD都是直角,∠BOC=60°,
∴∠AOB=30°,
∴∠AOD=120°;
②猜想∠BOC+∠AOD=180°.
证明:∵∠BOC=90°,
∴∠AOD=∠BOD+∠AOB=90°+∠AOB,
∵∠AOC=90°,
∴∠AOD+∠BOC=∠BOD+∠AOC=90°+90°=180°;
(2)类比②可得:∠AOD+∠BOC=∠BOD+∠AOC,
∵∠BOD=∠AOC=x°,∠AOD=y°,
∴∠BOC=(2x﹣y)°.
故答案为:120°.


科目:初中数学 来源: 题型:
【题目】在日历上,我们可以发现其中某些数满足一定的规律,如图是2017年12月份的日历.如图所选择的两组四个数,分别将每组数中相对的两数相乘,再相减,例如:7×9﹣1×15= ,18×20﹣12×26= ,不难发现,结果都是 .

(1)请将上面三个空补充完整;
(2)我们发现选择其他类似的部分规律也相同,请你利用整式的运算对以上的规律加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将笔记本活页一角折过去,使角的顶点A落在![]() 处,BC为折痕。
处,BC为折痕。
(1)图①中,若∠1=30°,求∠![]() 的度数;
的度数;
(2)如果又将活页的另一角斜折过去,使BD边与BA重合,折痕为BE,如图②所示,∠1=30°,求∠2以及∠![]() 的度数;
的度数;
(3)如果在图②中改变∠1的大小,则![]() 的位置也随之改变,那么问题(2)中∠
的位置也随之改变,那么问题(2)中∠![]() 的大小是否改变?请说明理由。
的大小是否改变?请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
(1)如图1,点D,E在AB,AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)
(2)如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.

(3)如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点.
①若BD=![]() ,求四边形BCDE的面积;
,求四边形BCDE的面积;
②若AB=3,AD=2,设CD2=x,EB2=y,求y与x之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
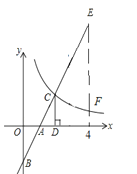
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A,B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②![]() ;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某房地产开发公司计划建![]() 、
、![]() 两种户型的住房共80套,该公司所筹资金不少于
两种户型的住房共80套,该公司所筹资金不少于![]() 万元,但不超过
万元,但不超过![]() 万元,且所筹资金全部用于建房,两种户型的建房的成本和售价如表:
万元,且所筹资金全部用于建房,两种户型的建房的成本和售价如表:
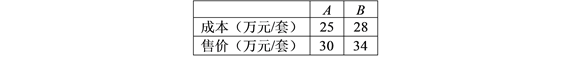
(![]() )该公司对这两种户型住房有哪几种方案?
)该公司对这两种户型住房有哪几种方案?
(![]() )该公司如何建房获利利润最大?
)该公司如何建房获利利润最大?
(![]() )根据市场调查,每套
)根据市场调查,每套![]() 型住房的售价不会改变,每套
型住房的售价不会改变,每套![]() 型住房的售价将会提高
型住房的售价将会提高![]() 万元
万元![]() ,且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?
,且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线 y=![]() x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在第一内作等腰 Rt△ABC,∠BAC=90. 点 P 是 x 轴上的一个动点,设 P(x,0).
(1)当 x =______________时,PB+PC 的值最小;
(2)当 x =______________时,|PB-PC|的值最大.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校原有600张旧课桌急需维修,经过A、B、C三个工程队的竞标得知,A、B的工作效率相同,且都为C队的2倍,若由一个工程队单独完成,C队比A队要多用10天.学校决定由三个工程队一齐施工,要求至多6天完成维修任务.三个工程队都按原来的工作效率施工2天时,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,A、B队提高的工作效率仍然都是C队提高的2倍.这样他们至少还需要3天才能完成整个维修任务.
(1)求工程队A原来平均每天维修课桌的张数;
(2)求工程队A提高工作效率后平均每天多维修课桌张数的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com