(1)解:∵∠A=50°,
∴∠C=

(180°-∠A)=

(180°-50°)=65°,
∵EG⊥BC,
∴∠CEG=90°-∠C=90°-65°=25°,
∵∠A=50°,∠D=30°,
∴∠CEF=∠A+∠D=50°+30°=80°,
∴∠GEF=∠CEF-∠CEG=80°-25°=55°;
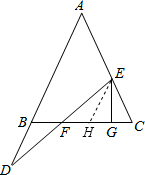
(2)证明:过点E作EH∥AB交BC于H,
则∠ABC=∠EHC,∠D=∠FEH,
∵AB=AC,
∴∠ABC=∠C,
∴∠EHC=∠C,
∴EC=EH,
∵BD=CE,
∴BD=EH,
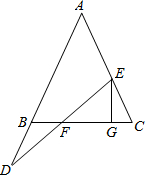
在△BDF和△HEF中,
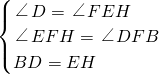
,
∴△BDF≌△HEF(AAS),
∴BF=FH,
又∵EC=EH,EG⊥BC,
∴CG=HG,
∴FG=FH+HG=BF+CG.
分析:(1)根据等腰三角形两底角相等求出∠C,再根据直角三角形两锐角互余求出∠CEG,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠CEF,然后计算即可得解;
(2)过点E作EH∥AB交BC于H,根据两直线平行,同位角相等可得∠ABC=∠EHC,内错角相等可得∠D=∠FEH,然后求出∠EHC=∠C,再根据等角对等边可得EC=EH,然后求出BD=EH,再利用“角角边”证明△BDF和△HEF全等,根据全等三角形对应边相等可得BF=FH,根据等腰三角形三线合一的性质可得CG=HG,即可得证.
点评:本题考查了等腰三角形的性质,全等三角形的判定与性质,主要利用了等腰三角形两底角相等的性质,等角对等边的性质,(2)作辅助线构造出全等三角形是解题的关键.

 如图,在△ABC中,AB=AC,E在线段AC上,D在AB的延长线,连DE交BC于F,过点E作EG⊥BC于G.
如图,在△ABC中,AB=AC,E在线段AC上,D在AB的延长线,连DE交BC于F,过点E作EG⊥BC于G. (180°-∠A)=
(180°-∠A)= (180°-50°)=65°,
(180°-50°)=65°,
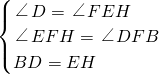 ,
,

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为