【题目】如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积．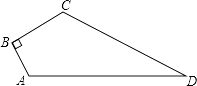 
【答案】解：连接AC，如图所示：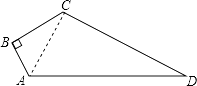 
∵∠B=90°，
∴△ABC为直角三角形，
又∵AB=3，BC=4，
∴根据勾股定理得：AC= 
=5，
又∵CD=12，AD=13，
∴AD2=132=169，CD2+AC2=122+52=144+25=169，
∴CD2+AC2=AD2 ，
∴△ACD为直角三角形，∠ACD=90°，
则S四边形ABCD=S△ABC+S△ACD= 
ABBC+ ACCD= ×3×4+ ×5×12=36．
故四边形ABCD的面积是36．
【解析】连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠C=90°，以AC为一边向外作等边三角形ACD，点E为AB的中点，连结DE．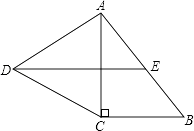 
（1）证明DE∥CB；
（2）探索AC与AB满足怎样的数量关系时，四边形DCBE是平行四边形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某小型企业实行工资与业绩挂钩制度，工人工资分为A、B、C、D四个档次．小明对该企业三月份工人工资进行调查，并根据收集到的数据，绘制了如下尚不完整的统计表与扇形统计图．
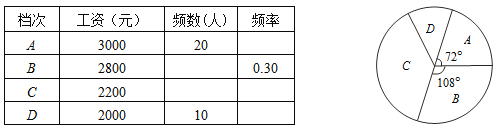
根据上面提供的信息，回答下列问题：
（1）求该企业共有多少人？
（2）请将统计表补充完整；
（3）扇形统计图中“C档次”的扇形所对的圆心角是 度.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE=DF，∠A=∠D，AB=DC．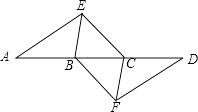 
（1）求证：四边形BFCE是平行四边形；
（2）若AD=10，DC=3，∠EBD=60°，则BE=时，四边形BFCE是菱形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】方程4x2＝81化成一元二次方程的一般形式后，其中的二次项系数、一次项系数和常数项分别是（ ）
A.4，0，81B.﹣4，0，81C.4，0，﹣81D.﹣4，0，﹣81
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
