
【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE. 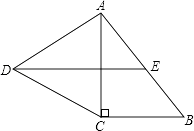
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
【答案】
(1)证明:连结CE.
∵点E为Rt△ACB的斜边AB的中点,
∴CE= ![]() AB=AE.
AB=AE.
∵△ACD是等边三角形,
∴AD=CD.
在△ADE与△CDE中, 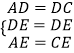 ,
,
∴△ADE≌△CDE(SSS),
∴∠ADE=∠CDE=30°.
∵∠DCB=150°,
∴∠EDC+∠DCB=180°.
∴DE∥CB.
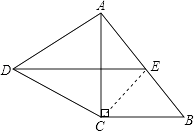
(2)解:当AC= ![]() AB或AB=2AC时,四边形DCBE是平行四边形,
AB或AB=2AC时,四边形DCBE是平行四边形,
理由:∵AC= ![]() AB,∠ACB=90°,
AB,∠ACB=90°,
∴∠B=30°,
∵∠DCB=150°,
∴∠DCB+∠B=180°,
∴DC∥BE,又∵DE∥BC,
∴四边形DCBE是平行四边形.
【解析】(1)首先连接CE,根据直角三角形的性质可得CE= ![]() AB=AE,再根据等边三角形的性质可得AD=CD,然后证明△ADE≌△CDE,进而得到∠ADE=∠CDE=30°,再有∠DCB=150°可证明DE∥CB;(2)当AC=
AB=AE,再根据等边三角形的性质可得AD=CD,然后证明△ADE≌△CDE,进而得到∠ADE=∠CDE=30°,再有∠DCB=150°可证明DE∥CB;(2)当AC= ![]() AB或AB=2AC时,四边形DCBE是平行四边形.根据(1)中所求得出DC∥BE,进而得到四边形DCBE是平行四边形.
AB或AB=2AC时,四边形DCBE是平行四边形.根据(1)中所求得出DC∥BE,进而得到四边形DCBE是平行四边形.
【考点精析】本题主要考查了等边三角形的性质和平行四边形的判定的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
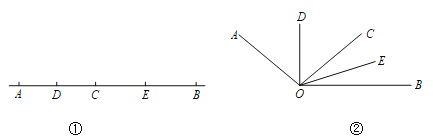
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(1,2),B(2,1),C(﹣1,﹣3).D(﹣2,3),其中不可能与点E(1,3)在同一函数图象上的一个点是( )
A. 点A B. 点B C. 点C D. 点D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程![]() 有两个不相等实数根的概率.
有两个不相等实数根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com