练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（1）已知2x=3，2y=5，求2x+y的值；

    （2）x﹣2y+1=0，求：2x÷4y×8的值．

    【答案】（1）15；（2）4

    【解析】

    （1）直接利用同底数幂的乘法运算法则将原式变形求出答案；
    （2）直接利用同底数幂的除法运算法则将原式变形求出答案．

    解：（1）∵2x=3，2y=5，∴2x+y=2x×2y=3×5=15；

    （2）∵x﹣2y+1=0，∴x﹣2y=﹣1，∴2x÷4y×8

    =2x﹣2y+3

    =22

    =4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】“龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场．图中的函数图象刻画了“龟兔再次赛跑”的故事（x表示乌龟从起点出发所行的时间，y1表示乌龟所行的路程，y2表示兔子所行的路程）．有下列说法： ①“龟兔再次赛跑”的路程为1000米；
    ②兔子和乌龟同时从起点出发；
    ③乌龟在途中休息了10分钟；
    ④兔子在途中750米处追上乌龟．
    其中正确的说法是 ． （把你认为正确说法的序号都填上）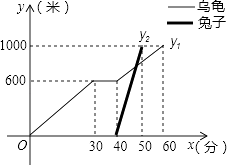

    查看答案和解析>>

    科目：初中数学 来源： 题型：

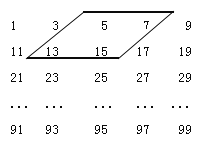
    【题目】如图所示的105（行列）的数阵，是由一些连续奇数组成的，形如图框中的四个数，设第一行的第一个数为．

    （1）用含的式子表示另外三个数；

    （2）若这样框中的四个数的和是200，求出这四个数；

    （3）是否存在这样的四个数，它们的和为246？为什么？

    【答案】（1）x+2，x+8，x+10；（2）45，47,53,55；（3）不存在．

    【解析】试题分析：（1）观察图框中的四个数，根据这四个数之间的数量关系，直接写出答案即可；（2）根据框中的四个数的和是200，列出方程，解方程即可；（3）根据框中的四个数的和是246，列出方程，解方程，根据方程解得情况判断是否存在即可.

    试题解析：

    （1）．

    （2）根据题意得： ，

    解之得， ．

    ∴x+2=47，x+8=53，x+10=55.

    答：这四个数分别为45、47、53、55.

    （3）不存在．

    由.

    ．

    而奇数是整数，所以不存在满足条件的数．

    【题型】解答题
    【结束】
    25

    【题目】某单位计划购买电脑若干台，经了解同一型号市场预售价均为每台5000元．现有两商场优惠促销，甲商场：购买不超过2台按原价销售，超过2台的部分每台打7折；乙商场：每台均打8折．

    （1）若学校购买5台，哪家商场较优惠？购买7台呢？

    （2）买多少台时两商场所需费用一样多？

    （3）你知道学校怎样选购更省钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一组数据：5、－2、0、1、4的中位数是（ ）

    A. 0 B. －2 C. 1 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】命题中①平行于同一条直线的两条直线平行；②垂直于同一条直线的两条直线平行；③过一点有且只有一条直线与已知直线平行；④过一点有且只有一条直线与已知直线垂直.为真命题的是________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】比较2100与375的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先阅读，然后答题．

    阿基米德测皇冠的故事

    叙古拉国王艾希罗交给金匠一块黄金，让他做一顶王冠．王冠做成后，国王拿在手里觉得有点轻．他怀疑金匠掺了假，可是金匠以脑袋担保说没有，并当面拿秤来称，结果与原来的金块一样重．国王还是有些怀疑，可他又拿不出证据，于是把阿基米德叫来，要他来解决这个难题．回家后，阿基米德闭门谢客，冥思苦想，但百思不得其解．一天，他的夫人逼他洗澡．当他跳入池中时，水从池中溢了出来．阿基米德听到那哗哗哗的流水声，灵感一下子冒了出来．他从池中跳出来，连衣服都没穿，就冲到街上，高喊着："优勒加！优勒加！（意为发现了）"．夫人这回可真着急了，嘴里嘟囔着"真疯了，真疯了"，便随后追了出去．街上的人不知发生了什么事，也都跟在后面追着看．原来，阿基米德由澡盆溢水找到了解决王冠问题的办法：相同质量的相同物质泡在水里，溢出的水的体积应该相同．如果把王冠放到水了，溢出的水的体积应该与相同质量的金块的体积相同，否则王冠里肯定掺有假．阿基为德跑到王宫后立即找来一盆水，又找来同样重量的一块黄金，一块白银，分两次泡进盆里，白银溢出的水比黄金溢出的几乎要多一倍，然后他又把王冠和金块分别泡进水盆里，王冠溢出的水比金块多，显然王冠的质量不等于金块的质量，王冠里肯定掺了假．在铁的事实面前，金匠不得不低头承认，王冠里确实掺了白银．烦人的王冠之谜终于解开了．

    小明受阿基米德测皇冠的故事的启发，想要做以下的一个探究：

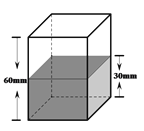
    小明准备了一个长方体的无盖容器和A，B两种型号的钢球若干．先往容器里加入一定量的水，如图，水高度为30mm，水足以淹没所有的钢球．

    探究一：小明做了两次实验，先放入3个A型号钢球，水面的高度涨到36mm；把3个A型号钢球捞出，再放入2个B型号钢球，水面的高度恰好也涨到36mm．

    由此可知A型号与B型号钢球的体积比为____________；

    探究二：小明把之前的钢球全部捞出，然后再放入A型号与B型号钢球共10个后，水面高度涨到57mm，问放入水中的A型号与B型号钢球各几个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A（x1，y1），B（x2，y2）在直线y＝kx+b上，且直线经过第一，二，三象限，当x1＞x2时，y1与y2的大小关系是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，以AC为一边向外作等边三角形ACD，点E为AB的中点，连结DE．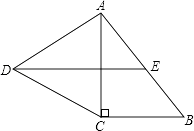

    （1）证明DE∥CB；
    （2）探索AC与AB满足怎样的数量关系时，四边形DCBE是平行四边形．

    查看答案和解析>>

    同步练习册答案