练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】命题中①平行于同一条直线的两条直线平行；②垂直于同一条直线的两条直线平行；③过一点有且只有一条直线与已知直线平行；④过一点有且只有一条直线与已知直线垂直.为真命题的是________.

    【答案】①④

    【解析】

    根据直线的性质，平行线公理，垂线的性质，以及平行线的性质对各小题分析判断即可．

    ①平行于同一条直线的两条直线平行，正确；

    ②应为在同一平面内，垂直于同一条直线的两条直线平行，故本小题错误；

    ③应为过直线外一点有且只有一条直线与已知直线平行，故本小题错误；

    ④过一点有且只有一条直线和已知直线垂直，正确.

    故答案为：①④.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，矩形纸片ABCD中，AB=6cm，BC=8cm，现将其沿EF对折，使得点C与点A重合，则EF长为cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC．

    （1）判断直线l与⊙O的位置关系，并说明理由；

    （2）若∠ABC的平分线BF交AD于点F，求证：BE=EF；

    （3）在（2）的条件下，若DE=4，DF=3，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某单位计划购买电脑若干台，经了解同一型号市场预售价均为每台5000元．现有两商场优惠促销，甲商场：购买不超过2台按原价销售，超过2台的部分每台打7折；乙商场：每台均打8折．

    （1）若学校购买5台，哪家商场较优惠？购买7台呢？

    （2）买多少台时两商场所需费用一样多？

    （3）你知道学校怎样选购更省钱？

    【答案】（1）购买5台，乙商场更优惠；购买7台，甲商场更优惠；（2）6；（3）答案见解析．

    【解析】试题分析：（1）根据甲乙两个商场的促销方案分别计算出学校购买5台和7台电脑所需的费用，比较即可；（2）设购买台时，两商场所需要费用一样多，根据费用一样多列出方程，解方程即可；（3）在（2）的基础上，比较即可.

    试题解析：

    （1）购买5台，甲商场：

    乙商场： ，， 乙商场更优惠．

    购买7台，甲商场：，乙商场： ．

    27500元＜28000元， 甲商场更优惠．

    （2）设购买台时，两商场所需要费用一样多，根据题意得

    ，解得： ．

    答：当购买台时，两商场所需要费用一样多．

    （3）当购买台数小于6时，在乙商场更省钱；

    当购买台数等于6时，两商场一样省钱；

    当购买台数大于6时，在甲商场更省钱．

    【题型】解答题
    【结束】
    26

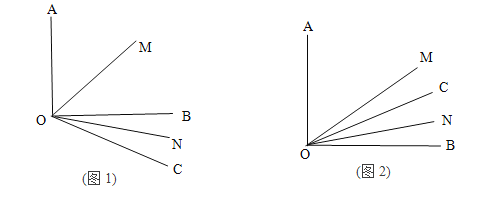
    【题目】已知∠AOB=90°，是锐角，ON平分，OM平分∠AOB．

    （1）如图1若=30°，求的度数？

    （2）若射线OC绕着点O运动到∠AOB的内部（如图2），在（1）的条件下求的度数；

    （3）若∠AOB=（90°≤＜180°），= （0°＜＜90°），请用含有的式子直接表示上述两种情况的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

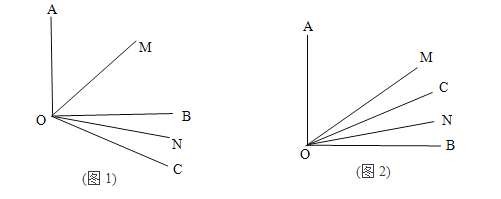
    【题目】已知∠AOB=90°，是锐角，ON平分，OM平分∠AOB．

    （1）如图1若=30°，求的度数？

    （2）若射线OC绕着点O运动到∠AOB的内部（如图2），在（1）的条件下求的度数；

    （3）若∠AOB=（90°≤＜180°），= （0°＜＜90°），请用含有的式子直接表示上述两种情况的度数．

    【答案】（1）60°；（2）30°；（3）①∠MON＝（＋），；②∠MON＝（－）．

    【解析】试题分析：（1）由于∠AOB=90°，∠BOC=30°，OM平分∠AOB，ON平分∠BOC，所以可以求得∠MOB和∠NOB的度数，进而求得∠MON的度数；（2）类比（1）的方法求解即可；（3）结合（1）（2）题的计算方法求解即可.

    试题解析：

    （1）∵OM平分∠AOB，ON平分∠BOC，

    ∴∠BOM＝∠AOB，∠BON＝∠BOC．

    ∵∠AOB＝90°，∠BOC＝30°，

    ∴∠BOM＝×90°＝45°，∠BON＝×30°＝15°，

    ∴∠MON＝∠BOM＋∠BON＝45°＋15°＝60°．

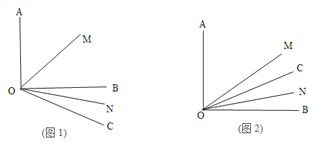
    （2）由（1）可知：∠BOM＝45°，∠BON＝15°，

    ∴∠MON＝∠BOM－∠BON＝45°－15°＝30°．

    （3）①∠MON＝（＋），②∠MON＝（－）．

    点睛：本题主要考查学生角平分线的定义及角的计算的理解和掌握，在解决角与角之间的关系时，要充分利用已知条件和图中的隐含条件.

    【题型】解答题
    【结束】
    27

    【题目】（1）已知线段AB=8cm，在线段AB上有一点C，且BC=4cm，M为线段AC的中点．

    ①求线段AM的长？

    ②若点C在线段AB的延长线上，AM的长度又是多少呢？

    （2）如图，AD=DB，E是BC的中点，BE=AC=2cm，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）已知2x=3，2y=5，求2x+y的值；

    （2）x﹣2y+1=0，求：2x÷4y×8的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）阅读理解：实数， ，∵，∴，即。若（为定值），则，当且仅当时等式成立，即时， ，∴当时， 取得 值（填“最大”或“最小”）。

    （2）理解应用：函数，当x= 时， 。

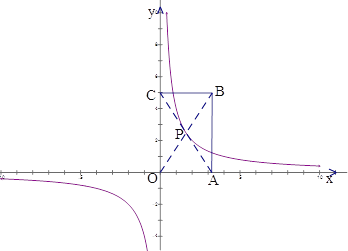
    （3）拓展应用：如图，双曲线经过矩形OABC的对角线交点P，求矩形OABC的最小周长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（　　）

    A.2x23x3＝6x6B.（﹣y2）3＝﹣y6

    C.2y3﹣6y2＝﹣4yD.（y﹣2）2＝y2﹣4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，已知线段AB=12cm，点C为线段AB上的一动点，点D，E分别是AC和BC中点.

    （1）若点C恰好是AB的中点，则DE=_______cm；

    （2）若AC=4cm，求DE的长；

    （3）试说明无论AC取何值（不超过12cm），DE的长不变；

    （4）如图②，已知∠AOB=120°，过角的内部任一点C画射线OC.若OD，OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.

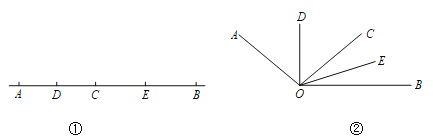
    查看答案和解析>>

    同步练习册答案