
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
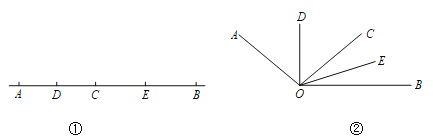
【答案】(1)6cm;(2)6cm;(3)理由见解析;(4)理由见解析.
【解析】试题分析:(1)由中点的定义即可解答;
(2)先求出BC的长,再由中点定义即可解答;
(3)由中点定义可得:DE=![]() AB,只与AB的长有关;
AB,只与AB的长有关;
(4)由角平分线的定义可得:∠DOE=![]() ∠AOB,即可得出结论.
∠AOB,即可得出结论.
试题解析:解:(1)∵AB=12cm,C点为AB的中点,∴AC=BC=6cm.
∵点D、E分别是AC和BC的中点,∴CD=CE=3cm,∴DE=6cm.
(2)∵AB=12cm,AC=4cm,∴BC=8cm.
∵点D、E分别是AC和BC的中点,∴CD=2cm,CE=4cm,∴DE=6cm;
(3)设AC=acm.∵点D、E分别是AC和BC的中点,∴DE=CD+CE=![]() AB=6cm,∴不论AC取何值(不超过12cm),DE的长不变;
AB=6cm,∴不论AC取何值(不超过12cm),DE的长不变;
(4)∵OD、OE分别平分∠AOC和∠BOC,∴∠DOE=∠DOC+∠COE=![]() ∠AOB.
∠AOB.
∵∠AOB=120°,∴∠DOE=60°,∴∠DOE的度数与射线OC的位置无关.


科目:初中数学 来源: 题型:
【题目】命题中①平行于同一条直线的两条直线平行;②垂直于同一条直线的两条直线平行;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直.为真命题的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.
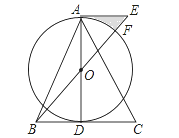
(1)求证:AE是⊙O的切线;
(2)若BD=![]() AD=4,求阴影部分的面积.
AD=4,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32. 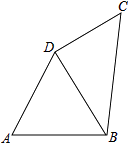
(1)求∠BDC的度数;
(2)四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE. 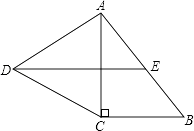
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国现行的个人所得税法自2011年9月1日起施行,其中规定个人所得税纳税办法如下:
一、以个人每月工资收入额减去3500元后的余额作为其每月应纳税所得额;
二、个人所得税纳税税率如下表所示:
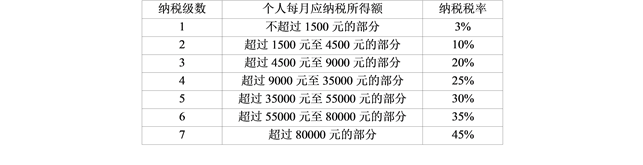
(1)若甲、乙两人的每月工资收入额分别为4500元和6000元,请分别求出甲、乙两人的每月应缴纳的个人所得税;
(2)若丙每月缴纳的个人所得税为85元,则丙每月的工资收入额应为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com