
【题目】(12分)如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.
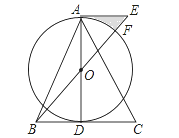
(1)求证:AE是⊙O的切线;
(2)若BD=![]() AD=4,求阴影部分的面积.
AD=4,求阴影部分的面积.
 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.

(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:实数![]() ,
, ![]() ,∵
,∵![]() ,∴
,∴![]() ,即
,即![]() 。若
。若![]() (
(![]() 为定值),则
为定值),则![]() ,当且仅当
,当且仅当![]() 时等式成立,即
时等式成立,即![]() 时,
时, ![]() ,∴当
,∴当![]() 时,
时, ![]() 取得 值(填“最大”或“最小”)。
取得 值(填“最大”或“最小”)。
(2)理解应用:函数![]() ,当x= 时,
,当x= 时, ![]() 。
。
(3)拓展应用:如图,双曲线![]() 经过矩形OABC的对角线交点P,求矩形OABC的最小周长。
经过矩形OABC的对角线交点P,求矩形OABC的最小周长。
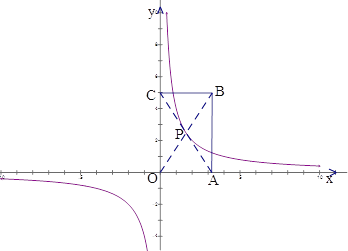
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=12cm,点C为线段AB上的一动点,点D,E分别是AC和BC中点.
(1)若点C恰好是AB的中点,则DE=_______cm;
(2)若AC=4cm,求DE的长;
(3)试说明无论AC取何值(不超过12cm),DE的长不变;
(4)如图②,已知∠AOB=120°,过角的内部任一点C画射线OC.若OD,OE分别平分∠AOC和∠BOC.试说明∠DOE的度数与射线OC的位置无关.
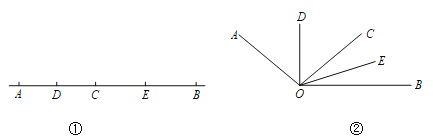
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,
①四边形ACED是平行四边形;
②△BCE是等腰三角形;
③四边形ACEB的周长是10+2 ![]() ;
;
④四边形ACEB的面积是16.
则以上结论正确的是( )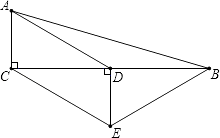
A.①②③
B.①②④
C.①③④
D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com