
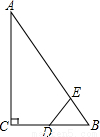
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
2或3.5或4.5.
【解析】
试题分析:∵Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,
∴AB=2BC=4(cm),
∵BC=2cm,D为BC的中点,动点E以1cm/s的速度从A点出发,
∴BD=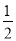 BC=1(cm),BE=AB-AE=4-t(cm),
BC=1(cm),BE=AB-AE=4-t(cm),
若∠BED=90°,
当A→B时,∵∠ABC=60°,
∴∠BDE=30°,
∴BE=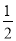 BD=
BD=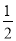 (cm),
(cm),
∴t=3.5,
当B→A时,t=4+0.5=4.5.
若∠BDE=90°时,
当A→B时,∵∠ABC=60°,
∴∠BED=30°,
∴BE=2BD=2(cm),
∴t=4-2=2,
当B→A时,t=4+2=6(舍去).
综上可得:t的值为2或3.5或4.5.
考点:相似三角形的判定与性质;含30度角的直角三角形.


科目:初中数学 来源:[同步]2015年课时同步练习(人教版)八年级数学下册18.1(解析版) 题型:选择题
(2013哈尔滨)如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )

A.4
B.3
C.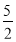
D.2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期期末考试数学试卷(解析版) 题型:解答题
(14分)如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).
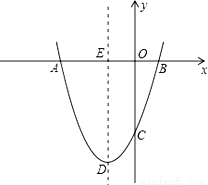
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期期末考试数学试卷(解析版) 题型:填空题
在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为 m.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系中,抛物线y=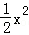 经过平移得到抛物线y=
经过平移得到抛物线y=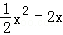 ,其对称轴与两段抛物线所围成的阴影部分的面积为( ).
,其对称轴与两段抛物线所围成的阴影部分的面积为( ).
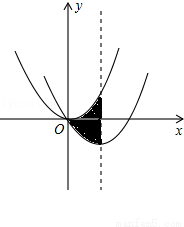
A.2 B.4 C.8 D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com