练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．已知x1，x2是方程2x2+4x-1=0的两个实数根，求$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$的值．

    分析 由韦达定理可得x1+x2=-2，x1x2=-$\frac{1}{2}$，代入到$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{（x}_{1}+{x}_{2}）^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$即可得答案．

    解答 解：∵x1，x2是方程2x2+4x-1=0的两个实数根，
    ∴x1+x2=-2，x1x2=-$\frac{1}{2}$，
    则$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{（x}_{1}+{x}_{2}）^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{4+1}{-\frac{1}{2}}$=-10．

    点评 本题主要考查根与系数的关系，熟练掌握韦达定理是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．计算：
    （1）（2x+y-1）•（2x-y+1）
    （2）$\frac{2x}{5x-3}$÷$\frac{3}{{25{x^2}-9}}$•$\frac{x}{5x+3}$
    （3）$\sqrt{1\frac{2}{3}}$÷$\sqrt{2\frac{1}{3}}$×$\sqrt{1\frac{1}{5}}$
    （4）$\frac{a}{a+2}$-$\frac{4}{{{a^2}+2a}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，MN是⊙O的直径．
    （1）用直尺和圆规作⊙O的内接正方形ABCD，并使其对边AD、BC都垂直于MN（不写作法，保留作图痕迹）；
    （2）连接MA、MB，求∠MAD、∠MBC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．若x=a+1是不等式$\frac{1}{2}x$-1＜2的解，则a＜5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知a，b满足b-a=-2014，求代数式[（a+b）（a-b）-（a-b）2-2b（b-a）]÷4b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知对于任意实数x，kx2-2x+k恒为正数，求实数k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

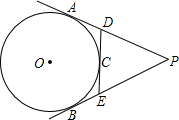    11．如图，PA、PB分别切⊙O于A、B两点，过劣弧$\widehat{AB}$上的一点C作⊙O的切线分别交PA、PB于D、E．求证：∠DOE=90°-$\frac{1}{2}$∠P．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．上海世博会区间，某博物馆每周都吸引大量中外游客前来参观，如果游客过多，对馆中的珍贵文物会产生不利影响，但同时考虑到文物的修缮和保存费用问题，还要保证一定的门票收入．因此，博物馆采取了涨浮门票价格的方法来控制参观人数，在该方法实施过程中发现：每周参观人数与票价之间存在着如图所示的一次函数关系，在这样的情况下．
    （1）如果确保每周4万元的门票收入，那么每周应限定参观人数是多少？门票价格应是多少元？
    （2）门片价格应该是多少元时门票收入最大，这样每周应有多少人参观？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图所示，点P是射线OC上任意一点，PD⊥OA于点D，PE⊥OB于点E，当OC平分∠AOB时，可以得到PD=PE，反过来，当PD=PE时，OC平分∠AOB吗？为什么？

    查看答案和解析>>

    同步练习册答案