
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 轴,
轴, ![]() 交
交![]() 于点
于点![]() .
.
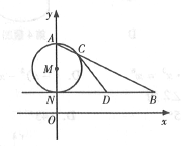
(1)若点![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若![]() 为线段
为线段![]() 的中点,求证:直线
的中点,求证:直线![]() 是
是![]() 的切线.
的切线.
【答案】(1)(![]() ,2);(2)详见解答.
,2);(2)详见解答.
【解析】
试题分析:(1)在直角三角形ABN中,求出BN的长,即可得到点B的坐标;(2)连接MC,NC,用等腰三角形的性质证明∠MCD=∠MND.
试题解析:(1)∵A的坐标为(0,6),N(0,2),∴AN=4,
∵∠ABN=30°,∠ANB=90°,∴AB=2AN=8,
∴由勾股定理可知:NB=![]() ,∴B(
,∴B(![]() ,2)
,2)
(2)连接MC,NC
∵AN是⊙M的直径,∴∠ACN=90°,∴∠NCB=90°,

在Rt△NCB中,D为NB的中点,
∴CD=![]() NB=ND,∴∠CND=∠NCD,
NB=ND,∴∠CND=∠NCD,
∵MC=MN,∴∠MCN=∠MNC.
∵∠MNC+∠CND=90°,∴∠MCN+∠NCD=90°,
即MC⊥CD. ∴直线CD是⊙M的切线.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】一艘轮船以16海里/时的速度离开港口(如图),向北偏东40°方向航行,另一艘轮船在同时以12海里/时的速度向北偏西一定的角度的航向行驶,已知它们离港口一个半小时后相距30海里(即BA=30),问另一艘轮船的航行的方向是北偏西多少度?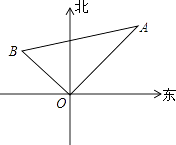
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO中,∠ABO=90°,其顶点O为坐标原点,点B在第二象限,点A在x轴负半轴上.若BD⊥AO于点D,OB= ![]() ,AB=2
,AB=2 ![]() ,则点A的坐标为 , 点B的坐标为 .
,则点A的坐标为 , 点B的坐标为 . 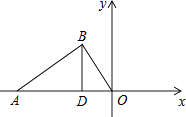
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=CD,则∠BEC的度数为( ) 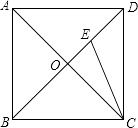
A.22.5°
B.60°
C.67.5°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一副”弦图“,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1 , S2 , S3 , 若S1+S2+S3=18,则正方形EFGH的面积为 . 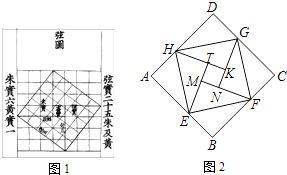
查看答案和解析>>
科目:初中数学 来源: 题型:
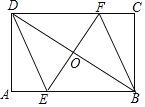
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com