
【题目】如图,一次函数y=kx+b(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)

(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由点A的坐标结合反比例函数系数k的几何意义,即可求出m的值;
(2)设点B的坐标为(n,![]() ),将一次函数解析式代入反比例函数解析式中,利用根与系数的关系可找出n、k的关系,由三角形的面积公式可表示出来b、n的关系,再由点A在一次函数图象上,可找出k、b的关系,联立3个等式为方程组,解方程组即可得出结论.
),将一次函数解析式代入反比例函数解析式中,利用根与系数的关系可找出n、k的关系,由三角形的面积公式可表示出来b、n的关系,再由点A在一次函数图象上,可找出k、b的关系,联立3个等式为方程组,解方程组即可得出结论.
(1)∵点A(4,1)在反比例函数![]() 的图象上,
的图象上,
∴m=4×1=4,
∴反比例函数的解析式为![]() .
.
(2)∵点B在反比例函数![]() 的图象上,
的图象上,
∴设点B的坐标为(n,![]() ).
).
将y=kx+b代入![]() 中,得:kx+b=
中,得:kx+b=![]() ,
,
整理得:![]() ,∴4n=
,∴4n=![]() ,即nk=﹣1①.
,即nk=﹣1①.
令y=kx+b中x=0,则y=b,
即点C的坐标为(0,b),
∴S△BOC=![]() bn=3,∴bn=6②.
bn=3,∴bn=6②.
∵点A(4,1)在一次函数y=kx+b的图象上,
∴1=4k+b③.
联立①②③成方程组,即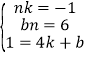 ,解得:
,解得: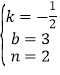 ,
,
∴该一次函数的解析式为![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】如图,∠ACB=∠ADB=90°,M、N 分别是 AB、CD 的中点.

(1)求证:MN⊥CD;
(2)若 AB=50,CD=48,求 MN 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场要建一个饲养场(矩形ABCD)两面靠现有墙(AD位置的墙最大可用长度为27米,AB位置的墙最大可用长度为15米),另两边用木栏围成,中间也用木栏隔开,分成两个场地及一处通道,并在如图所示的三处各留1米宽的门(不用木栏).建成后木栏总长45米.设饲养场(矩形ABCD)的一边AB长为x米.

(1)饲养场另一边BC=____米(用含x的代数式表示).
(2)若饲养场的面积为180平方米,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小刚拿着老师的等腰直角三角板玩,一不小心掉到垂直地面的两个木块之间,如图所示:

(1)求证:△ADC≌△CEB;
(2)若测得AD=15cm,BE=10cm,求两个木块之间的距离DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
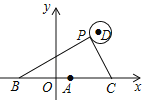
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线![]() 相交于A(1,
相交于A(1,![]() ),B(4,0)两点.
),B(4,0)两点.

(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线L经过点A,BD⊥直线L,CE⊥直线L,垂足分别为点D、E.证明:DE=BD+CE.
(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线L上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图③,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:I是EG的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC 中,∠A=90°,现要在 AC 边上确定一点 D,使点 D到 BA、BC 的距离相等.

(1)请你按照要求,在图上确定出点 D 的位置(尺规作图,不写作法,保留作图痕迹);
(2)若 BC=10,AB=8,则 AC= ,AD= (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则下列说法正确的有(____)
①DC′平分∠BDE;②BC长为![]() ;③△
;③△![]() 是等腰三角形;④△CED的周长等于BC的长.
是等腰三角形;④△CED的周长等于BC的长.

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com