
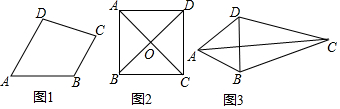
���� ��1�����á����ڱ��ı��Ρ��Ķ��������������ɣ�
��2���þ��κ����ε��ж������жϳ��ı��μ��Ǿ��Σ��������Σ��Ӷ��õ����������Σ�
��3�����жϳ���ACF�ס�ABD���õ�CF=$\sqrt{5}$BD���������CBF=90�㣬����ù��ɶ���������⣮
��� ��1���⣺����������AB=BC���������£�
���ı���ABCD���ı��Σ���AB=BC��
���ı���ABCD�ǡ����ڱ��ı��Ρ���
�ʴ�Ϊ��AB=BC��
��2��֤�����߶Խ���AC��BD����ƽ�֣�
���ı���ABCD��ƽ���ı���
�֡�AC=BD��
���ABCD�Ǿ���
�֡�AB=AD��
�����ABCD��������
��3���⣺BC2+CD2=5BD2���������£�
��AB=AD��
�ཫ��ADC���Ƶ�A��ת����ABF������CF����ͼ��ʾ��
���С�ABF�ա�ADC��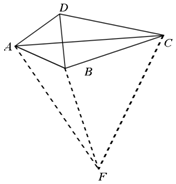 ���ABF=��ADC����BAF=��DAC��AF=AC��FB=CD��
���ABF=��ADC����BAF=��DAC��AF=AC��FB=CD��
�ڡ�ACF�͡�ADB�У�
�ߡ�BAD=��CAF��$\frac{AC}{AD}=\frac{AF}{AB}$��
���ACF�ס�ADB��
��$\frac{CF}{BD}=\frac{AC}{AB}$��
��AC=$\sqrt{5}$AB��
��CF=$\sqrt{5}$BD��
�ߡ�BAD+��BCD=90�㣬
���ABC+��ADC=270��
����ABC+��ABF=270�㣬
���CBF=90�㣬
��BC2+FB2=CF2=��$\sqrt{5}$BD��2=5BD2��
��BC2+CD2=5BD2��
���� �������ı����ۺ��⣬��Ҫ�������¶�������⣬���Σ����Σ������ε����ʺ��ж������ɶ�����������ȫ�Ⱥ����Ƶ����ʺ��ж����Ȿ��Ĺؼ������������߷ֱ��жϳ����������ƺ�ȫ�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��BD=2AD��E��F��G�ֱ���OC��OD��AB���е㣮���н��ۣ���EG=EF�� �ڡ�EFG�ա�GBE�� ��FBƽ�֡�EFG����EAƽ�֡�GEF�����ı���BEFG�����Σ�������ȷ���Ǣ٢ڢܣ�
ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��BD=2AD��E��F��G�ֱ���OC��OD��AB���е㣮���н��ۣ���EG=EF�� �ڡ�EFG�ա�GBE�� ��FBƽ�֡�EFG����EAƽ�֡�GEF�����ı���BEFG�����Σ�������ȷ���Ǣ٢ڢܣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڵ�����ABC�У�AB=AC=5���뾶Ϊ1�ġ�O�ֱ���AB��AC������E��F���㣬BG�ǡ�O�����ߣ��е�ΪG����BG�ij�Ϊ$\frac{11}{3}$��
��ͼ���ڵ�����ABC�У�AB=AC=5���뾶Ϊ1�ġ�O�ֱ���AB��AC������E��F���㣬BG�ǡ�O�����ߣ��е�ΪG����BG�ij�Ϊ$\frac{11}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com