
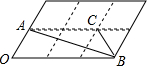
 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 如图,连接EA、EC,先证明∠AEC=90°,E、C、B共线,再根据tan∠ABC=$\frac{AE}{EB}$,求出AE、EB即可解决问题.
解答 解:如图,连接EA,EC,
设菱形的边长为a,由题意得∠AEF=30°,∠BEF=60°,AE=$\sqrt{3}$a,EB=2a,
∴∠AEC=90°,
∵∠ACE=∠ACG=∠BCG=60°,
∴∠ECB=180°,
∴E、C、B共线,
在Rt△AEB中,tan∠ABC=$\frac{AE}{EB}$=$\frac{\sqrt{3}a}{2a}$=$\frac{\sqrt{3}}{2}$.
故选D.
点评 本题考查菱形的性质,三角函数、特殊三角形边角关系等知识,解题的关键是添加辅助线构造直角三角形解决问题,属于中考常考题型.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{a}^{2}+{b}^{2}}{a+b}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a+b}$ | C. | $\frac{a-b}{{a}^{2}-2ab+{b}^{2}}$ | D. | $\frac{6x}{8y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BC⊥CA于点C,DC⊥CE点C,∠ACE=∠DCB,BC=CA,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.
如图,BC⊥CA于点C,DC⊥CE点C,∠ACE=∠DCB,BC=CA,DC=CE,直线BD与AE交于点F,交AC于点G,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 从中随机抽取1张,抽到黑桃的可能性更大 | |
| B. | 从中随机抽取1张,抽到黑桃和红桃的可能性一样大 | |
| C. | 从中随机抽取5张,必有2张红桃 | |
| D. | 从中随机抽取7张,可能都是红桃 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com