
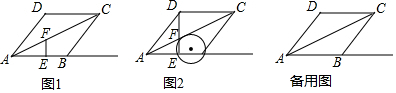
分析 (1)如图1中,作DH⊥AB于H.在Rt△ADH中,由∠AHD=90°,AD=5,cos∠DAH=$\frac{3}{5}$,推出AH=3,DH=$\sqrt{{5}^{2}-{3}^{2}}$=4,即可解决问题;
(2)分三种情形分别求解:①如图2中,当⊙O与直线DF相切时.②如图3中,当⊙O与AC相切时.③如图4中,当⊙O与CD相切于点M.分别求解即可.
解答 解:(1)如图1中,作DH⊥AB于H.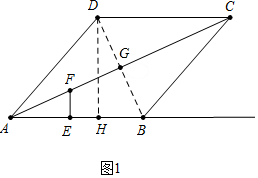
在Rt△ADH中,∵∠AHD=90°,AD=5,cos∠DAH=$\frac{3}{5}$,
∴AH=3,DH=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴S菱形ABCD=AB•DH=5×4=20.
(2)①如图2中,当⊙O与直线DF相切时,易知,∠BFD=90°,DF=BF.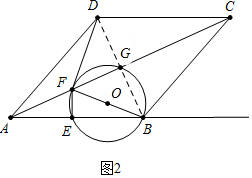
∵BD=2$\sqrt{5}$,
∴BF=$\sqrt{10}$.
设EF=x,则AE=2EF=2x,
在Rt△BEF中,∵BF2=EF2+BE2,
∴10=x2+(5-2x)2,
解得x=1或3,
∴AE=2或6时,⊙O与直线DF相切.
②如图3中,当⊙O与AC相切时,易知点F与G重合,设EF=x,AE=2x,
在Rt△AFE中,∵AG2=AE2+GE2,
∴20=4x2+x2,
∴x2=4,
∴x=2,
∴AE=4时,⊙O与直线CF相切.
③如图4中,当⊙O与CD相切于点M,延长MO交AE与H,设EF=x,则AE=2x,则OH=$\frac{1}{2}$EF=$\frac{1}{2}$x,BF=$\sqrt{{x}^{2}+(2x-5)^{2}}$,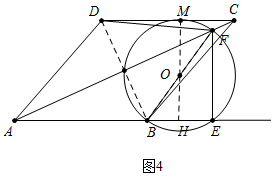
∵HM=4,
∴OM+OH=4,
∴$\frac{1}{2}$$\sqrt{{x}^{2}+(2x-5)^{2}}$+$\frac{1}{2}$x=4,
整理得,4x2-4x-39=0,
解得x=$\frac{1+2\sqrt{10}}{2}$或x=$\frac{1-2\sqrt{10}}{2}$(舍弃),
∴AE=1+2$\sqrt{10}$,
综上所述,满足条件的AE的值为2或4或6或1+2$\sqrt{10}$.
点评 本题考查圆综合题、菱形的性质、直线与圆的位置关系、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,学会构建方程解决问题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
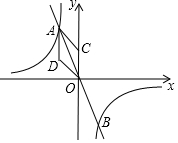 如图,反比例函数$y=\frac{k}{x}$与y=mx交于A,B两点,设点A、B的坐标分别为A(x1,y1),B(x2,y2),S=|x1y1|,且$\frac{3}{s-1}=\frac{4}{s}$,
如图,反比例函数$y=\frac{k}{x}$与y=mx交于A,B两点,设点A、B的坐标分别为A(x1,y1),B(x2,y2),S=|x1y1|,且$\frac{3}{s-1}=\frac{4}{s}$,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
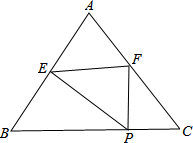 如图,已知,等腰△ABC中,AB=AC=5,BC=6,点P在BC上(与B,C不重合),作PE⊥AB,垂足是E,PF⊥BC,交AC于F,设PC=x,△PEF面积为y.
如图,已知,等腰△ABC中,AB=AC=5,BC=6,点P在BC上(与B,C不重合),作PE⊥AB,垂足是E,PF⊥BC,交AC于F,设PC=x,△PEF面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
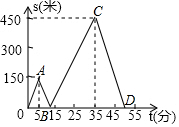 甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示.
甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲、乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
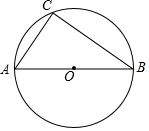 已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.
已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.73×108 | B. | 4.73×109 | C. | 4.73×1010 | D. | 4.73×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.323×105 | B. | 1.323×104 | C. | 1.3×105 | D. | 1.323×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
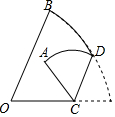 如图,在扇形AOB中,∠AOB=60°,AO=6,点D为$\widehat{AB}$的中点,C为半径OA上一动点(点A除外),沿CD对折后点A恰好落在扇形AOB的边线OB或OA上,AC的长可以是6-3$\sqrt{3}$或6或9-3$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=60°,AO=6,点D为$\widehat{AB}$的中点,C为半径OA上一动点(点A除外),沿CD对折后点A恰好落在扇形AOB的边线OB或OA上,AC的长可以是6-3$\sqrt{3}$或6或9-3$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com