
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转α°,分别交直线BC、AD于点E、F.

(1)当α= °,四边形ABEF是平行四边形;
(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形.
①α= °,构造的四边形是菱形;
②若构造的四边形是矩形,求出该矩形的面积.
【答案】(1)当α=90°,四边形ABEF是平行四边形(2)①45或90②![]()
【解析】
(1)由AB⊥AC得到∠BAC=90°,然后根据平行四边形的对角线互相平分,可得AB=OA=2,即△AOB是等腰直角三角形,则∠AOB=45°,再根据平行四边形的判定,当EF∥AB时,四边形ABEF是平行四边形,可得EF⊥AC,根据旋转的性质可得α=90°;
(2)①同(1)的判断,由菱形的判定可得到α的度数;
②先根据勾股定理求出BC的长,然后根据同一个三角形的面积的不同求法,得到平行线间的距离,由矩形的判定与性质,可得分情况求解.
(1) 90°;
(2)① 45°或90°;
②∵AB⊥AC,AB=2,AC=4,∴BC=2![]() ,
,
根据条件,可得AD与BC的距离h=![]() .
.
如图①,

当EF=AC时,四边形AECF为矩形,矩形AECF的对角线长为4,
∴![]() ,
,
∴矩形AECF的面积=![]() .
.
如图②,

当EF=BD时,四边形AECF为矩形,矩形AECF的对角线长为4![]() ,
,
∴![]() ,
,
∴矩形AECF的面积=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技馆对学生参观实行优惠,个人票为每张6元,另有团体票可售,票价45元,每票最多限10人入馆参观.
(1)如果参观的学生人数36人,至少应付多少元?
(2)如果参观的学生人数为48人,至少应付多少元?
(3)如果参观的学生人数为一个两位数![]() (a表示十位上的数字,b表示个位上的数字),用含a、b的代数式表示至少应付给科技馆的总金额.
(a表示十位上的数字,b表示个位上的数字),用含a、b的代数式表示至少应付给科技馆的总金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台球是一项高雅的体育运动,其中包含了许多物理、几何学知识,图-①是一个台球桌,目标球F与本球之间有一个G球阻挡.


(1)击球者想通过击打E球,让E球先撞球台的AB边,经过一次反弹后再撞击F球,他应将E球打到AB边上的哪一点?请在图10-①中用尺规作出这一点H,并作出E球的运行路线;(不写画法,保留作图痕迹)
(2)如图-②,现以D为原点,建立直角坐标系,记A(0,4),C(8,0),E(4,3),F(7,1),求E球按刚才方式运行到球的路线长度(忽略球的大小)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形纸片ABC的面积为48,BC的长为8.按下列步骤将三角形纸片ABC进行裁剪和拼图:
第一步:如图1,沿三角形ABC的中位线DE将纸片剪成两部分.在线段DE上任意取一点F,在线段BC上任意取一点H,沿FH将四边形纸片DBCE剪成两部分;
第二步:如图2,将FH左侧纸片绕点D旋转180°,使线段DB与DA重合;将FH右侧纸片绕点E旋转180°,使线段EC与EA重合,再与三角形纸片ADE拼成一个与三角形纸片ABC面积相等的四边形纸片.


图1 图2
(1)当点F,H在如图2所示的位置时,请按照第二步的要求,在图2中补全拼接成的四边形;
(2)在按以上步骤拼成的所有四边形纸片中,其周长的最小值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列说法错误的是( ).
①∠1和∠3是同位角;②∠1和∠5是同位角;③∠1和∠2是同旁内角;④∠1和∠4是内错角.
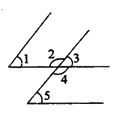
A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过A(0,2),B(4,0)两点.
(1)求直线AB对应的函数解析式;
(2)将该直线向上平移6个单位,求平移后的直线与x轴交点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com