
【题目】某科技馆对学生参观实行优惠,个人票为每张6元,另有团体票可售,票价45元,每票最多限10人入馆参观.
(1)如果参观的学生人数36人,至少应付多少元?
(2)如果参观的学生人数为48人,至少应付多少元?
(3)如果参观的学生人数为一个两位数![]() (a表示十位上的数字,b表示个位上的数字),用含a、b的代数式表示至少应付给科技馆的总金额.
(a表示十位上的数字,b表示个位上的数字),用含a、b的代数式表示至少应付给科技馆的总金额.
【答案】(1)171(元);(2)至少付225元(3)至少应付(45a+45)元.
【解析】
试题分析:(1)若参观的学生人数36人,则应买3张团体票,买6张个人票.
(2)参观的学生人数为48人,分两种情况进行计算,买5张团体票应付225元,买4张团体票,8张个人票应付228元,故至少应付225元.
(3)应分类讨论,当0≤b≤7,且为整数时,至少应付(45a+6b)元;当8≤b≤9,且为整数时,至少应付(45a+45)元.
解:(1)若参观的学生人数36人,则应付费用:3×45+6×6=171(元)
(2)参观的学生人数为48人,如买4张团体,8张个人票,应付:4×45+6×8=228(元),
若买5张团体票,应付:5×45=225<228,∴至少付225元.
(3)当0≤b≤7,且为整数时,至少应付(45a+6b)元;
当8≤b≤9,且为整数时,至少应付(45a+45)元.


科目:初中数学 来源: 题型:
【题目】列方程解应用题
情景:

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需___________元,购买12根跳绳需_____________元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,平行四边形纸片ABCD中,AD=5,S甲行四边形纸片ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为
A.平行四边形
B.菱形
C.矩形
D.正方形
(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.
求证:四边形AFF′D是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.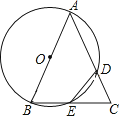
(1)求证:AB=AC;
(2)若AB=4,BC=2 ![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题: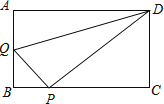
(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( ) 
A.10
B.8 ![]()
C.4 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转α°,分别交直线BC、AD于点E、F.

(1)当α= °,四边形ABEF是平行四边形;
(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形.
①α= °,构造的四边形是菱形;
②若构造的四边形是矩形,求出该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一慢车和一快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,试根据图象回答下列问题:

(1)由图象你可以得到哪些信息?
(2)求慢车、快车的速度.
(3)求A,B两地之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com