
【题目】(1)如图1,平行四边形纸片ABCD中,AD=5,S甲行四边形纸片ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为
A.平行四边形
B.菱形
C.矩形
D.正方形
(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.
求证:四边形AFF′D是菱形.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
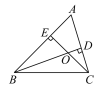
【题目】如图,在△ABC中,BD是AC边上的高,CE是AB边上的高,BD与CE相交于点O,则∠ABD___∠ACE(填“>”“<”或“=”),∠A+∠DOE=___度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;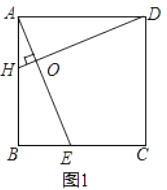
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;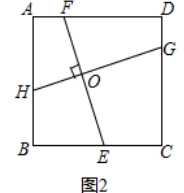
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.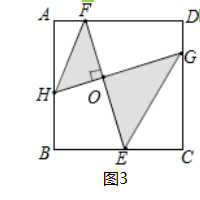
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y= ![]() x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K. 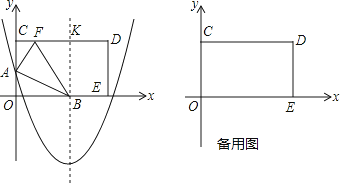
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为(),BK的长是 , CK的长是
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2 , 在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为( ![]() ,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 . 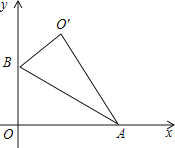
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技馆对学生参观实行优惠,个人票为每张6元,另有团体票可售,票价45元,每票最多限10人入馆参观.
(1)如果参观的学生人数36人,至少应付多少元?
(2)如果参观的学生人数为48人,至少应付多少元?
(3)如果参观的学生人数为一个两位数![]() (a表示十位上的数字,b表示个位上的数字),用含a、b的代数式表示至少应付给科技馆的总金额.
(a表示十位上的数字,b表示个位上的数字),用含a、b的代数式表示至少应付给科技馆的总金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列说法错误的是( ).
①∠1和∠3是同位角;②∠1和∠5是同位角;③∠1和∠2是同旁内角;④∠1和∠4是内错角.
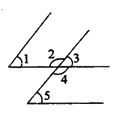
A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com