
【题目】提出问题:
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;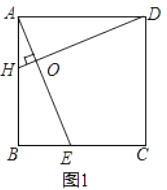
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;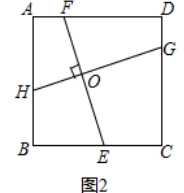
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.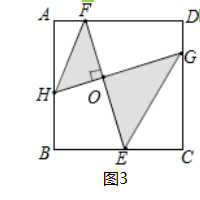
【答案】
(1)
解:∵四边形ABCD是正方形,
∴AB=DA,∠ABE=90°=∠DAH.
∴∠HAO+∠OAD=90°.
∵AE⊥DH,
∴∠ADO+∠OAD=90°.
∴∠HAO=∠ADO.
∴△ABE≌△DAH(ASA),
∴AE=DH.
(2)
解:EF=GH.
将FE平移到AM处,则AM∥EF,AM=EF.
将GH平移到DN处,则DN∥GH,DN=GH.
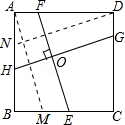
∵EF⊥GH,
∴AM⊥DN,
根据(1)的结论得AM=DN,所以EF=GH
(3)
解:∵四边形ABCD是正方形,
∴AB∥CD
∴∠AHO=∠CGO
∵FH∥EG
∴∠FHO=∠EGO
∴∠AHF=∠CGE
∴△AHF∽△CGE
∴ ![]()
∵EC=2
∴AF=1
过F作FP⊥BC于P,
根据勾股定理得EF= ![]() ,
,
∵FH∥EG,
∴ ![]()
根据(2)知EF=GH,
∴FO=HO.
∴ ![]() ,
,
![]() ,
,
∴阴影部分面积为 ![]() .
.

【解析】(1)由正方形的性质得AB=DA,∠ABE=90°=∠DAH.所以∠HAO+∠OAD=90°,又知∠ADO+∠OAD=90°,所以∠HAO=∠ADO,于是△ABE≌△DAH,可得AE=DH;(2)EF=GH.将FE平移到AM处,则AM∥EF,AM=EF,将GH平移到DN处,则DN∥GH,DN=GH.根据(1)的结论得AM=DN,所以EF=GH;(3)易得△AHF∽△CGE,所以 ![]() ,由EC=2得AF=1,过F作FP⊥BC于P,根据勾股定理得EF=
,由EC=2得AF=1,过F作FP⊥BC于P,根据勾股定理得EF= ![]() ,因为FH∥EG,所以
,因为FH∥EG,所以 ![]() ,根据(2)①知EF=GH,所以FO=HO,再求得三角形FOH与三角形EOG的面积相加即可.
,根据(2)①知EF=GH,所以FO=HO,再求得三角形FOH与三角形EOG的面积相加即可.
【考点精析】本题主要考查了勾股定理的概念和正方形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
分组 | 划记 | 频数 |
2.0<x≤3.5 | 正正 | 11 |
3.5<x≤5.0 |
| 19 |
5.0<x≤6.5 | ||
6.5<x≤8.0 | ||
8.0<x≤9.5 |
| 2 |
合计 | 50 |
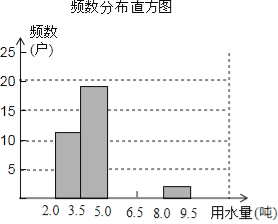
(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图①,若AB∥CD,点P在AB,CD外部,则有 ∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
情景:

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需___________元,购买12根跳绳需_____________元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地治理水质,保护环境,我县污水处理公司决定购买10台污水处理设备,现有A、B两种设备可供选择,月处理污水分别为240m3/月、200m3/月,经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)若污水处理公司购买设备的预算资金不超过105万元,你认为该公司有哪几种购买方案?
(2)若每月需处理的污水约2040m3,在不突破资金预算的前提下,为了节约资金,又要保证治污效果,请你为污水处理公司设计一种最省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,平行四边形纸片ABCD中,AD=5,S甲行四边形纸片ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为
A.平行四边形
B.菱形
C.矩形
D.正方形
(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.
求证:四边形AFF′D是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( ) 
A.10
B.8 ![]()
C.4 ![]()
D.2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com