
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图①,若AB∥CD,点P在AB,CD外部,则有 ∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
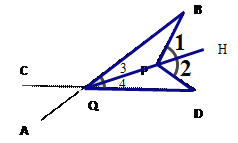
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
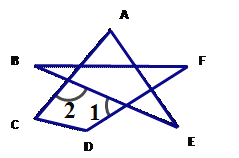
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.

【答案】(1)不成立(2)∠BPD=∠BQD+∠B+∠D(3)∠A+∠B+∠C+∠D+∠E=180°
【解析】
【试题分析】(1)利用两直线平行,内错角相等,得:PE//AB,则![]() ;利用平行线的传递性,得:PE//AB,AB//CD,所以PE//CD,再次利用利用两直线平行,内错角相等,得:PE//CD,则
;利用平行线的传递性,得:PE//AB,AB//CD,所以PE//CD,再次利用利用两直线平行,内错角相等,得:PE//CD,则![]() ,利用等量代换得:∠BPD=
,利用等量代换得:∠BPD=![]() =∠B+∠D.即∠BPD=∠B+∠D.
=∠B+∠D.即∠BPD=∠B+∠D.
(2)利用三角形的外角等于不相邻的两个内角和,得![]() ,再利用角度转化即可.即
,再利用角度转化即可.即![]() =
=![]() .
.
(3)利用转化的思想,利用外角的性质,将6个角的和转化为四边形的内角和,即360°.
【试题解析】
(1)不成立,∠BPD=∠B+∠D.
理由:如图,作PE//AB,则![]() ,因为AB//CD,所以PE//CD,则
,因为AB//CD,所以PE//CD,则![]() ,所以∠BPD=
,所以∠BPD=![]() =∠B+∠D.即∠BPD=∠B+∠D.
=∠B+∠D.即∠BPD=∠B+∠D.
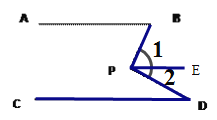
(2)作射线QP,![]() ,则
,则![]() =
=![]() .
.
即:![]() =
=![]() .
.
(3)由题意得:![]() ,得∠A+∠B+∠C+∠D+∠E+∠F=∠C+∠D+
,得∠A+∠B+∠C+∠D+∠E+∠F=∠C+∠D+![]() =360°.
=360°.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】八年级(1)班同学上数学活动课,利用角尺平分一个角(如图).设计了如下方案:
(Ⅰ)∠AOB是一个任意角,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与M,N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(Ⅱ)∠AOB是一个任意角,在边OA,OB上分别取OM=ON,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与M,N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线.
(1)方案(Ⅰ)、方案(Ⅱ)是否可行?若可行,请证明;若不可行,请说明理由.
(2)在方案(Ⅰ)PM=PN的情况下,继续移动角尺,同时使PM⊥OA,PN⊥OB.此方案是否可行?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了两幅尚不完整的统计图,如图所示,请根据统计图中所提供的信息解答下列问题: 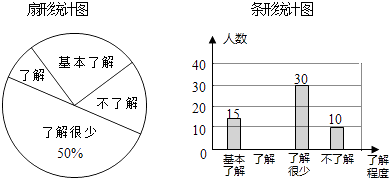
(1)接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;
(2)请补全条形统计图;
(3)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD是AC边上的高,CE是AB边上的高,BD与CE相交于点O,则∠ABD___∠ACE(填“>”“<”或“=”),∠A+∠DOE=___度.
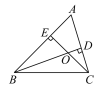
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
请结合图表完成下列各题:
(1)①求表中a的值;②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率. 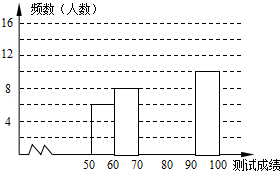
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元. 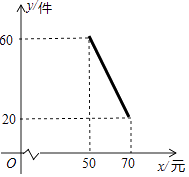
(1)当售价在50~70元时,求每月销售量为y与x的函数关系式?
(2)当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
(3)若该商店每月采购这种新商品的进货款不低于1760元,则该商品每月最大利润为元.
查看答案和解析>>
科目:初中数学 来源: 题型:
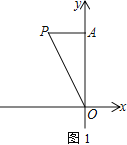
【题目】如图,平面直角坐标系中,已知点A(0,5),点P(m,5)在第二象限,连接AP、OP
(1) 如图1,若OP=6,求m的值
(2) 如图2,点C在x轴负半轴上,以CP为斜边作直角三角形BCP,∠CBP=90°,且∠BPC=∠APO.取OC的中点D,连接AD、BD,求证:AD=BD
(3) 如图3,将△AOP沿直线OP翻折得到△EOP(点A的对应点为点E).若点E到x轴的距离不大于3,直接写出m的取值范围(无需解答过程)
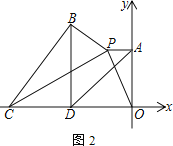
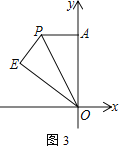
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;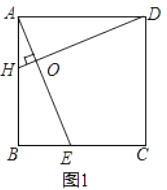
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;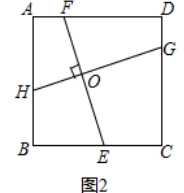
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.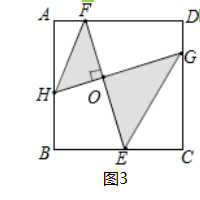
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为( ![]() ,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 . 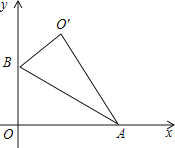
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com