
【题目】某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同.当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元. 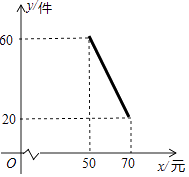
(1)当售价在50~70元时,求每月销售量为y与x的函数关系式?
(2)当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
(3)若该商店每月采购这种新商品的进货款不低于1760元,则该商品每月最大利润为元.
【答案】
(1)解:令y=kx+b
由图知:当x=50时,y=60;当x=70时,y=20.
∴ ![]() ,
,
∴ ![]() ,
,
∴y=﹣2x+160(50≤x≤70);
(2)解:由题可知,
当40≤x≤50时,Q=60(x﹣40)=60x﹣2400,
∵60>0,
∴Q随x的增大而增大,
∴x=50时,Q有最大值600元.
当50≤x≤70时,Q=y(x﹣40)=2x2+240x﹣6400=﹣2(x﹣60)2+800,
∵﹣2<0,
∴x=60时,Q有最大值800元.
综上所述,当该商品售价是60元时,该商店每月获利最大,最大利润是800元.
(3)792
【解析】解:(3)设采购的数量为m,则40m≥1760,解得m≥44, 由(1)知,若40≤x≤50,则利润的最大值为600元;
若50≤x≤70,由﹣2x+160≥44可得x≤58,
∵Q=﹣2(x﹣60)2+800中x<60时,Q随x的增大而增大,
∴当x=58时,Q取得最大值,最大值为792,
故答案为:792.
(1)待定系数法求解可得;(2)分40≤x≤50和50≤x≤70两种情况,根据总利润=单件利润×销售量列出函数解析式,根据函数性质解答可得;(3)由进货款求得进货量的范围,结合(2)中的函数解析式分类讨论求解可得.


科目:初中数学 来源: 题型:
【题目】下列命题中:![]() 有公共顶点和一条公共边的两个角一定是邻补角;
有公共顶点和一条公共边的两个角一定是邻补角;![]() 垂线段最短;
垂线段最短;![]() 经过直线外一点,有且只有一条直线与这条直线平行;
经过直线外一点,有且只有一条直线与这条直线平行;![]() 相等的角是对顶角;
相等的角是对顶角;![]() 等角的余角相等,其中假命题的个数是
等角的余角相等,其中假命题的个数是![]()
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
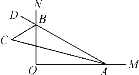
【题目】如图,∠MON=90°,点A,B分别在射线OM,ON上移动,∠OAB的平分线与∠OBA的外角平分线交于点C,试猜想:随着点A,B的移动,∠ACB的大小是否发生变化,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图①,若AB∥CD,点P在AB,CD外部,则有 ∠B=∠BOD,又因为∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,请说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论;
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某华为手机专卖店销售5台甲型手机和8台乙型手机的利润为1600元,销售15台甲型手机和6台乙型手机的利润为3000元
(1) 求每台甲型手机和乙型手机的利润
(2) 专卖店计划购进两种型号的华为手机共120台,其中乙型手机的进货量不低于甲型手机的2倍.设购进甲型手机x台,这120台手机全部销售的销售总利润为y元
① 直接写出y关于x的函数关系式_______________,x的取值范围是_______________
② 该商店如何进货才能使销售总利润最大?说明原因
(3) 专卖店预算员按照(2)中的方案准备进货,同时专卖店对甲型手机销售价格下调a元,结果预算员发现无论按照哪种进货方案最后销售总利润不变.请你判断有这种可能性吗?如果有,求出a的值;如果没有,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
情景:

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需___________元,购买12根跳绳需_____________元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com