
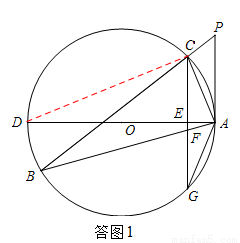
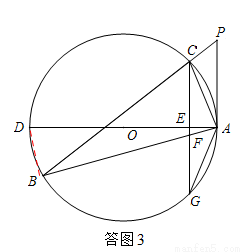
如图,△ABC的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD于E,交AB于F,交⊙O于G。
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AF·AB;
(3)若⊙O的直径为10,AC=2 ,AB=4
,AB=4 ,求△AFG的面积.
,求△AFG的面积.

(1)PA与⊙O相切,理由见解析;(2)证明见解析;(3)3.
【解析】
试题分析:(1)连接CD,由AD为⊙O的直径,可得∠ACD=90°,由圆周角定理,证得∠B=∠D,由已知∠PAC=∠B,可证得DA⊥PA,继而可证得PA与⊙O相切.
(2)连接BG,易证得△AFG∽△AGB,由相似三角形的对应边成比例,证得结论.
(3)连接BD,由AG2=AF•AB,可求得AF的长,易证得△AEF∽△ABD,即可求得AE的长,继而可求得EF与EG的长,则可求得答案.
试题解析:【解析】
(1)PA与⊙O相切.理由如下:
如答图1,连接CD,
∵AD为⊙O的直径,∴∠ACD=90°.
∴∠D+∠CAD=90°.
∵∠B=∠D,∠PAC=∠B,∴∠PAC=∠D.
∴∠PAC+∠CAD=90°,即DA⊥PA.
∵点A在圆上,
∴PA与⊙O相切.
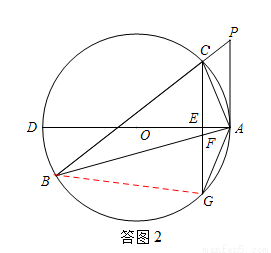
(2)证明:如答图2,连接BG,
∵AD为⊙O的直径,CG⊥AD,∴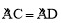 .∴∠AGF=∠ABG.
.∴∠AGF=∠ABG.
∵∠GAF=∠BAG,∴△AGF∽△ABG.
∴AG:AB=AF:AG. ∴AG2=AF•AB.
(3)如答图3,连接BD,
∵AD是直径,∴∠ABD=90°.
∵AG2=AF•AB,AG=AC=2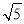 ,AB=4
,AB=4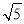 ,∴AF=
,∴AF=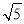 .
.
∵CG⊥AD,∴∠AEF=∠ABD=90°.
∵∠EAF=∠BAD,∴△AEF∽△ABD. ∴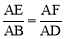 ,即
,即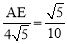 ,解得:AE=2.
,解得:AE=2.
∴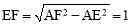 .
.
∵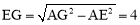 ,∴
,∴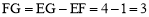 .
.
∴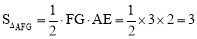 .
.
考点:1. 圆周角定理;2.直角三角形两锐角的关系;3. 相切的判定;4.垂径定理;5.相似三角形的判定和性质;6.勾股定理;7.三角形的面积.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源:2014年初中毕业升学考试(广西贺州卷)数学(解析版) 题型:填空题
如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西河池卷)数学(解析版) 题型:选择题
如图,点A,点B的坐标分别是 ,将线段AB绕A旋转180°后得到线段AC,则点C的坐标为( )
,将线段AB绕A旋转180°后得到线段AC,则点C的坐标为( )

A. B.
B.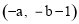 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西河池卷)数学(解析版) 题型:选择题
如图,a∥b,∠1=55°,∠2=65°,则∠3的大小是( )

A.50° B.55° C.60° D.65°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西崇左卷)数学(解析版) 题型:解答题
如图,在四边形ABCD中,对角线AC,BD相交于点O,且AC⊥BD,点E,F,G,H分别是AB,BC,CD,DA的中点,依次连接各边中点得到四边形EFGH,求证:四边形EFGH是矩形.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西南宁卷)数学(解析版) 题型:选择题
数据1,2,4,0,5,3,5的中位数和众数分别是 ( )
(A)3和2 (B)3和3 (C)0和5 (D)3和5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com