
如图,O为直线AB上一点,OC平分∠BOD,OE⊥OC,垂足为O,∠AOE与∠DOE有什么关系,请说明理由.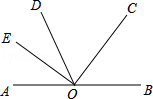
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
已知AB∥CD,分别探讨下列四个图形中∠APC和∠A、∠C的关系,并选择图(1)、(2)之一说明理由。 (10分)
(1) (2) (3) (4)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
数学课老师提出这样一个问题:已知如图,直线AB//CD,直线EF与直线AB交于G,与直线CD交于H,且GN平分 ,求证:
,求证: .
.
下面是某同学给出一种证法,请你将解答中缺少的条件、结论或证明理由补充完整.
证明: (已知)
(已知)
 (_________________________)
(_________________________) AB//CD,EF与AB、CD分别交于G、H(已知)
AB//CD,EF与AB、CD分别交于G、H(已知)
 ( __________________________ )
( __________________________ ) 是
是 的平分线,(已知)
的平分线,(已知) _______
_______ (角平分线定义)
(角平分线定义) (已证)
(已证) (_________________)
(_________________) _______________________(已证)
_______________________(已证)  (等量代换)
(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于 CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是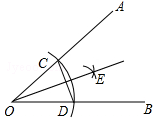
A.射线OE是∠AOB的平分线
B.△COD是等腰三角形
C.C、D两点关于OE所在直线对称
D.O、E两点关于CD所在直线对称
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
填写推理理由
如图,已知AD⊥BC于D,EF⊥BC于F,AD平分∠BAC.将∠E=∠1的过程填写完整.
解:解:∵AD⊥BC, EF⊥BC( 已知 )
∴∠ADC=∠EFC= 90°( 垂直的意义 )
∴AD//EF
∴∠1= ( )
∠E= ( )
又∵AD平分∠BAC( 已知 )
∴ =
∴∠1=∠E.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就图①、图②、或图③中的一种情况,给出证明.
我选图 来证明.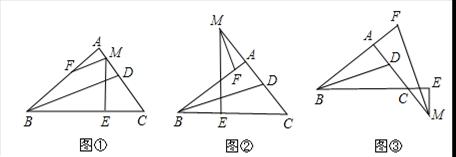
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com