
С����ѧϰ������֪ʶʱ����������������Ȥ�Ľ��ۣ���Rt��ABC�У���A=90�㣬BDƽ�֡�ABC��MΪֱ��AC��һ�㣬ME��BC������ΪE����AME��ƽ���߽�ֱ��AB�ڵ�F��
��1����ͼ�٣�MΪ��AC��һ�㣬��BD��MF��λ�ù�ϵ�� ��
��ͼ�ڣ�MΪ��AC�����ӳ�����һ�㣬��BD��MF��λ�ù�ϵ�� ��
��ͼ�ۣ�MΪ��AC�ӳ�����һ�㣬��BD��MF��λ�ù�ϵ�� ��
��2�����ͼ�١�ͼ�ڡ���ͼ���е�һ�����������֤����
��ѡͼ ��֤����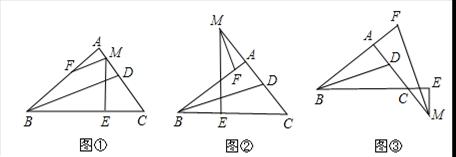
��1��BD��MF��BD��MF��BD��MF����2��֤����������
���������������1���ٸ�������֪��AME+��ABC=180�㣬�����ý�ƽ���ߵ����ʵá�AMF+��ABD=90��,����AMF+��AFM=90��,�Ӷ���AFM=��ABD����BD��MF��
����֤��AME=��ABC,��MF��BD�ֱ��ǡ�AME����ABC��ƽ���ߣ���֪��AMF=��ABD������ABD+��ADB=90�㣬���ԡ�AMF+��ADB=90�㣬��BD��MF��
�۷���ͬ��2����
(2)����ͬ��1����
(1)BD��MF��BD��MF��BD��MF��
(2)��1��BD��MF
�������£��ߡ�A=90�㣬ME��BC��
���ABC+��AME=360�㩁90���2=180�㣬
��BDƽ�֡�ABC��MFƽ�֡�AME��
���ABD=��ABC����AMF=��AME��
���ABD+��AMF=����ABC+��AME��=90�㣬
�֡ߡ�AFM+��AMF=90�㣬
���ABD=��AFM��
��BD��MF��
��2��BD��MF��
�������£��ߡ�A=90�㣬ME��BC��
���ABC+��C=��AME+��C=90�㣬
���ABC=��AME��
��BDƽ�֡�ABC��MFƽ�֡�AME��
���ABD=��AMF��
�ߡ�ABD+��ADB=90�㣬
���AMF+��ADB=90�㣬
��BD��MF��
��3��BD��MF��
�������£��ߡ�A=90�㣬ME��BC��
���ABC+��ACB=��AME+��ACB=90�㣬
���ABC=��AME��
��BDƽ�֡�ABC��MFƽ�֡�AME��
���ABD=��AMF��
�ߡ�AMF+��F=90�㣬
���ABD+��F=90�㣬
��BD��MF
���㣺1��ƽ���ߵ��ж���2����ֱ���ж���3���ı��ε��ڽǺͣ�


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��OΪֱ��AB��һ�㣬OCƽ�֡�BOD��OE��OC������ΪO����AOE���DOE��ʲô��ϵ����˵�����ɣ�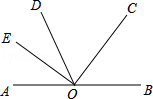
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��������֤����
��֪����ͼ��ʾ��BCE��AFE��ֱ�ߣ�
AB��CD����1=��2����3=��4��
��֤��AD��BE
֤������ AB��CD ����֪��
�� ��4 =�� �� ��
�� ��3 =��4 ����֪��
�� ��3 =�� �� ��
�ߡ�1 =��2 ����֪��
���1+��CAF =��2+ ��CAF ( )
������ =�� ��
�� ��3 =�� �� ��
�� AD��BE �� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��һ����������A��B���㣬��A��ʾ�� ����B��ʾ��6����P�Ǹ������ϵ�һ�����㣨����A��B�غϣ���ʾ��x����M��N�ֱ����߶�AP��BP���е㡣
����B��ʾ��6����P�Ǹ������ϵ�һ�����㣨����A��B�غϣ���ʾ��x����M��N�ֱ����߶�AP��BP���е㡣
��1�������P���߶�AB�ϣ����M��ʾ������ , ���N��ʾ������ ���ú�x �Ĵ���ʽ��ʾ�����������߶�MN�ij���
��2�������P�ڵ�B�Ҳ࣬��������߶�MN�ij���
��3�������P�ڵ�A��࣬���߶�MN�ij��Ȼ�ı�������ı䣬��˵�����ɣ�������䣬��ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�����������жϣ��١�A=��F���ڡ�C=��D���ۡ�1=��2������������������Ϊ����������һ����Ϊ���ۣ���һ��֤���Ⲣд��֤������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ʵ��֤��,ƽ�澵������ߵĹ�����:�䵽ƽ�澵�ϵĹ��ߺͱ�������Ĺ�����ƽ�澵���е�������. ��ͼ1,һ������m�䵽ƽ�澵a��,��a�����Ĺ���Ϊn�����������m���������n��ƽ�澵a���е���ǡ�1=��2.
(1) ��ͼ2,һ������m�䵽ƽ�澵a��,��a���䵽ƽ�澵b��,�ֱ�b����.����b������Ĺ���n�����mƽ��,�ҡ�1=50��,���2=_____��,��3=_____��. 
(2) ��(1)��m��n������1=55��,���3=______��;����1=40��,���3=______��.
(3) ��(1)��(2),������룺����ƽ�澵a��b�ļнǡ�3=______��ʱ,����ʹ�κ��䵽ƽ�澵a�ϵĹ���m,����ƽ�澵a��b�����η����,�������m�뷴�����nƽ��.����˵��������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij����Ӵ�Ӫ��P���������ر�ƫ��60��ǰ����3km����A�أ��������Ϸ���ǰ��3km����C�أ��ش��������⣺
��1����1cm����1ǧ�ף�����������н�·��ͼ��
��2��������C����Ӫ�ص�ʲô�����ϣ�����ȷ��1�㣩
��3�����������Ӵ�ʱ��Ӫ��ʵ�ʶ�Զ������ȷ��0.1ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��ʾ��ֱ��AB��CD��ֱ��AB��CD��ֱ��EF���أ�EGƽ�֡�BEF��FGƽ�֡�DFE��
��1������AEF=500,���EFG�Ķ�������4�֣�
��2���ж�EG��FG��λ�ù�ϵ����˵�����ɡ���6�֣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com