
实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等. 如图1,一束光线m射到平面镜a上,被a反射后的光线为n,则入射光线m、反射光线n与平面镜a所夹的锐角∠1=∠2.
(1) 如图2,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=_____°,∠3=_____°. 
(2) 在(1)中m∥n,若∠1=55°,则∠3=______°;若∠1=40°,则∠3=______°.
(3) 由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=______°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?
(1)100°,90°;(2)90°,90°;(3)90°,理由见解析.
解析试题分析:(1)根据入射角等于反射角得出∠1=∠4,∠5=∠7,求出∠6,根据平行线性质即可求出∠2,求出∠5,根据三角形南京和锻炼求出∠3即可;
(2)根据入射角等于反射角得出∠1=∠4,∠5=∠7,求出∠6,根据平行线性质即可求出∠2,求出∠5,根据三角形南京和锻炼求出∠3即可;
(3)求出∠4+∠5,求出∠1+∠4+∠5+∠7,即可求出∠2+∠6,根据平行线的判定推出即可.
试题解析:(1)如图:
∵∠1=50°,
∴∠4=∠1=50°,
∴∠6=180°-50°-50°=80°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=100°,
∴∠5=∠7=40°,
∴∠3=180°-50°-40°=90°,
(2)∵∠1=40°,
∴∠4=∠1=40°,
∴∠6=180°-40°-40°=100°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=80°,
∴∠5=∠7=50°,
∴∠3=180°-50°-40°=90°;
∵∠1=55°,
∴∠4=∠1=55°,
∴∠6=180°-55°-55°=70°,
∵m∥n,
∴∠2+∠6=180°,
∴∠2=110°,
∴∠5=∠7=35°,
∴∠3=180°-55°-35°=90°;
(3)当∠3=90°时,m∥n,
理由是:∵∠3=90°,
∴∠4+∠5=180°-90°=90°,
∵∠1=∠4,∠7=∠5,
∴∠1+∠4+∠5+∠7=2×90°=180°,
∴∠6+∠2=180°-(∠1+∠4)+180°-(∠5+∠7)=180°,
∴m∥n,
考点: 平行线的判定与性质.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:初中数学 来源: 题型:解答题
已知AB∥CD,分别探讨下列四个图形中∠APC和∠A、∠C的关系,并选择图(1)、(2)之一说明理由。 (10分)
(1) (2) (3) (4)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
填写推理理由
如图,已知AD⊥BC于D,EF⊥BC于F,AD平分∠BAC.将∠E=∠1的过程填写完整.
解:解:∵AD⊥BC, EF⊥BC( 已知 )
∴∠ADC=∠EFC= 90°( 垂直的意义 )
∴AD//EF
∴∠1= ( )
∠E= ( )
又∵AD平分∠BAC( 已知 )
∴ =
∴∠1=∠E.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就图①、图②、或图③中的一种情况,给出证明.
我选图 来证明.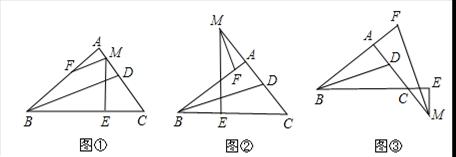
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知线段AB.
(1)用尺规作图的方法作出线段AB的垂直平分线CD(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的直线CD上任意取两点M,N(线段AB的上方).连结AM,AN,BM,BN.求证:∠MAN=∠MBN.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转 得△AB1C1,画出△AB1C1.
得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com