
如图所示,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE。
(1)若∠AEF=500,求∠EFG的度数。(4分)
(2)判断EG与FG的位置关系,并说明理由。(6分)
(1)25°。(2)可证明∠G=180°-(∠BEF+∠DFE)=90°,所以EG⊥FG
解析试题分析:.解:(!)∵AB∥CD
∴∠EFD=∠AEF=50°
∵FG平分∠DFE
∵∠EFG= ∠DFE=
∠DFE= ×50°=25°
×50°=25°
(2)EG⊥FG
理由:∵AB∥CD
∴∠BEF+∠EFD=180°
∵EG平分∠BEF,FG平分∠DFE
∴∠GEF= ∠BEF,∠GFE=
∠BEF,∠GFE= ∠DFE
∠DFE
∴∠GEF+∠GFE= ∠BEF+
∠BEF+ ∠DFE
∠DFE
= (∠BEF+∠DFE)
(∠BEF+∠DFE)
= ×180°
×180°
=90°
∴∠G=180°-(∠BEF+∠DFE)=90°
∴EG⊥FG
考点:平行线性质与垂线判定
点评:本题难度中等,主要考查学生对平行线性质及垂线性质定理判定等应用。为中考常考题型,注意数形结合应用。


科目:初中数学 来源: 题型:解答题
小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就图①、图②、或图③中的一种情况,给出证明.
我选图 来证明.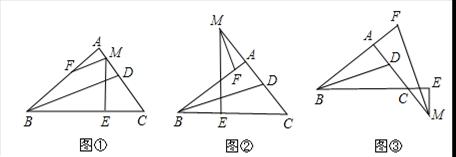
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(1)如图,直线l 、l
、l 分别与直线l
分别与直线l 、l
、l 相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
(2)如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并对此结论进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知△ABC和点O.
(1)把△ABC绕点O顺时针旋转900得到△A1B1C1,在网格中画出△A1B1C1;
(2)用直尺和圆规作△ABC的边AB,AC的垂直平分线,并标出两条垂直平分线的交点P(要求保留作图痕迹,不写作法);指出点P是△ABC的内心,外心,还是重心?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转 得△AB1C1,画出△AB1C1.
得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
在比例尺是1∶8 000的南京市城区地图上,太平南路的长度约为25 cm,它的实际长度约为( )
| A.320 cm | B.320 m |
| C.2 000 cm | D.2 000 m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com