
(1)如图,直线l 、l
、l 分别与直线l
分别与直线l 、l
、l 相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度数.
(2)如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并对此结论进行证明.
(1)112°;(2)∠AED=∠ACB
解析试题分析:(1)如图所示,由∠2+∠5=180°,∠2=104°,可求得∠5=76°,即可得到∠1=∠5,从而可以证得l ∥l
∥l ,根据平行线的性质可得∠4=∠6,再结合∠3=68°,∠3+∠6=180°求解;
,根据平行线的性质可得∠4=∠6,再结合∠3=68°,∠3+∠6=180°求解;
(2)先根据同角的补角相等可得∠2=∠EFD,即可证得AB∥EF,根据平行线的性质可得∠3=∠ADE,由∠3=∠B可得∠B=∠ADE,即可证得DE∥BC,从而可以求得结果.
解:(1)如图: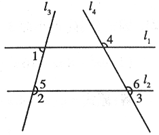
∵∠2+∠5=180°,∠2=104°,
∴∠5=76°.
∵∠1=76°.
∴∠1=∠5.
∴l ∥l
∥l
∴∠4=∠6.
∵∠3=68°,∠3+∠6=180°,
∴∠6=112°.
∴∠4=112°;
(2)∠AED=∠ACB
∵∠1+∠EFD=180°,∠1+∠2=180°
∴∠2=∠EFD
∴AB∥EF
∴∠3=∠ADE
∵∠3=∠B
∴∠B=∠ADE
∴DE∥BC
∴∠AED=∠ACB.
考点:平行线的判定和性质
点评:平行线的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.


科目:初中数学 来源: 题型:解答题
完成下面的证明.
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某考察队从营地P处出发,沿北偏东60°前进了3km到达A地,再向正南方向前进3km最后达C地.回答下列问题:
(1)用1cm代表1千米,画出考察队行进路线图;
(2)度量出C地在营地的什么方向上?(精确到1°)
(3)测算出考察队此时离营地实际多远?(精确到0.1千米)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,∠MON及边ON上一点A.在∠MON内部求作:点P,使得PA⊥ON,且点P到∠MON两边的距离相等.(请尺规作图,保留作图痕迹,不要求写出作法,不必证明).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图所示,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE。
(1)若∠AEF=500,求∠EFG的度数。(4分)
(2)判断EG与FG的位置关系,并说明理由。(6分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com