
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( ) 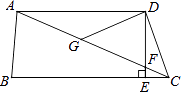
A.2 ![]()
B.![]()
C.2 ![]()
D.![]()
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A. 明年国庆节宁波的天气是晴天B. 小华上学的路上遇到同班同学
C. 任意掷一枚均匀的硬币,正面朝上D. 在学校操场上抛出的篮球会下落
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣22×7﹣(﹣3)×6+5;
(2)( ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )×24÷(﹣2);
)×24÷(﹣2);
(3)56×1 ![]() +56×(﹣
+56×(﹣ ![]() )﹣56×
)﹣56× ![]() ;
;
(4)(﹣1)4﹣ ![]() ×[2﹣(﹣3)2].
×[2﹣(﹣3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在同一直线噵路上同起点,同方向同进出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到达终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙距离终点______________米。
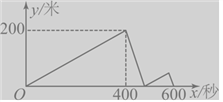
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式。心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质。我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如下图表:
四种气质类型人数频数分布表 | 黏液质气质各年级人数频数分布直方图 | |||||||||||||||
|
|
根据以上信息完成下列问题并补全频数分布直方图:
(1)![]() _______,
_______, ![]() _______
_______
(2)请你估计一下,高三年级1200名学生中,胆汁型和多血质的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
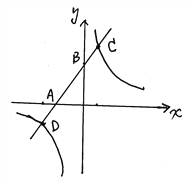
【题目】如图,反比例函数![]() (n为常数,
(n为常数, ![]() )的图象与一次函数
)的图象与一次函数![]() (k、b为常数,
(k、b为常数, ![]() )的图象在第一象限内交于点C
)的图象在第一象限内交于点C![]() ,一次函数
,一次函数![]() 与x轴、y轴分别交于A、B两点。已知
与x轴、y轴分别交于A、B两点。已知![]() ,
, ![]() 。
。
(1)求一次函数的解析式和反比例函数的解析式;
(2)若点P在x轴上且使得![]() 面积为
面积为![]() 面积的3倍,求满足条件的P点坐标。
面积的3倍,求满足条件的P点坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
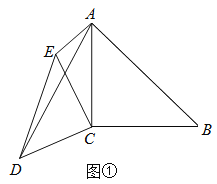
【题目】(1)如图①已知∠ACB=∠DCE=90°,AC=BC=4,CE=CD,AE=2,∠CAE=45°,求AD的长.
(2)如图②已知∠ACB=∠DCE=90°,∠ABC=∠DEC=∠CAE=30°,AC=2,AE=4![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知蜗牛从A点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“﹣”,从开始到结束爬行的各段路程(单位:cm)依次为:+7,﹣5,﹣10,﹣8,+9,﹣6,+12,+4
(1)若A点在数轴上表示的数为﹣3,则蜗牛停在数轴上何处,请通过计算加以说明;
(2)若蜗牛的爬行速度为每秒 ![]() cm,请问蜗牛一共爬行了多少秒?
cm,请问蜗牛一共爬行了多少秒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com