
分析 (1)根据概率公式直接计算;
(2)先画树状图展示所有12种等可能的结果数,再找出这2名同学恰好都是初一(2)班同学的结果数,然后根据概率公式求解.
解答 解:(1)被选中的这名同学恰好是初一(2)班同学的概率=$\frac{2}{4}$=$\frac{1}{2}$;
故答案为$\frac{1}{2}$;
(2)画树状图为:
共有12种等可能的结果数,其中这2名同学恰好都是初一(2)班同学的结果数为2,
所以这2名同学恰好都是初一(2)班同学的概率=$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了统计图.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:填空题
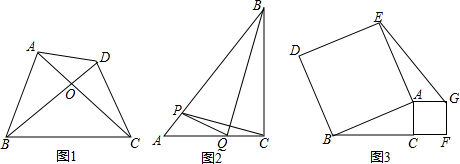
 如图所示,?ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE:AF=2:3,∠C=120°,则?ABCD的面积为24cm2.
如图所示,?ABCD的周长为20cm,AE⊥BC于点E,AF⊥CD于点F,AE:AF=2:3,∠C=120°,则?ABCD的面积为24cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
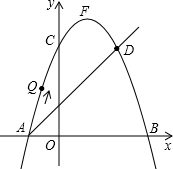 如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.
如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
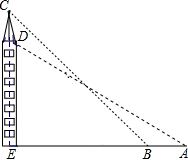 如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )
如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面的A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面的B处,又测得信号塔顶端C的仰角为45°,CD⊥AB于点E,E、B、A在一条直线上.信号塔CD的高度为( )| A. | 20$\sqrt{3}$ | B. | 20$\sqrt{3}$-8 | C. | 20$\sqrt{3}$-28 | D. | 20$\sqrt{3}$-20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
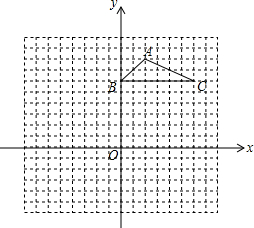 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
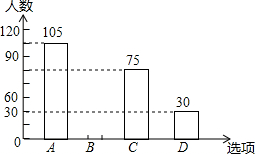 某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:| 选项 | 球类运动 | 百分比 |
| A | 乒乓球 | 35% |
| B | 羽毛球 | x |
| C | 篮球 | 25% |
| D | 其他 | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
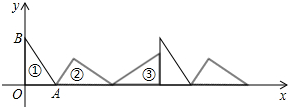 如图①,在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为($\frac{144}{5}$,$\frac{12}{5}$).
如图①,在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为($\frac{144}{5}$,$\frac{12}{5}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com