
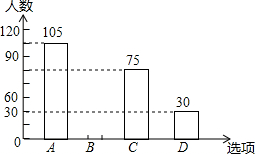
 某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:| 选项 | 球类运动 | 百分比 |
| A | 乒乓球 | 35% |
| B | 羽毛球 | x |
| C | 篮球 | 25% |
| D | 其他 | 10% |
分析 (1)结合统计图和统计表给出的数据即可求出抽查的学生人数;由各选项的百分比之和为100%即可求出x的值;进而可将条形统计图补充完整;
(2)由统计表可知喜欢篮球的人数占到25%,进而可估计该校喜爱“篮球”这项球类运动的学生约有多少人;
(3)画树状图得出所有等可能的情况数,找出恰好是甲与乙的情况,即可确定出所求概率.
解答 解:
(1)由统计图可知A的人数为105,由统计表可知A所占的比例式35%,所以总人数为105÷35%=300(人)
由已知条件可知x=1-35%-25%-10%=30%,
所以B的人数=300×30%=90(人),
将条形统计图补充完整如图所示:
故答案为:300,30%,
(2)估计该校喜爱“篮球”这项球类运动的学生约有1200×25%=300(人);
(3)画树状图,如图所示:
所有等可能的情况有12种,其中恰好是甲与丁的情况有2种,
所以所抽到的两人恰好是甲和丁的概率=$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力以及求随机事件的概率;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


科目:初中数学 来源: 题型:选择题
| A. | 0.37×105 | B. | 3.7×104 | C. | 37×103 | D. | 370×102 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
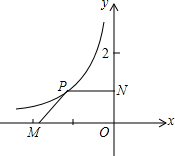 如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )
如图,平面直角坐标系中,点M是x轴负半轴上一定点,点P是函数y=-$\frac{1}{x}$,(x<0)上一动点,PN⊥y轴于点N,当点P的横坐标在逐渐增大时,四边形PMON的面积将会( )| A. | 逐渐增大 | B. | 始终不变 | C. | 逐渐减小 | D. | 先增后减 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1+(1-x)=1 | B. | 1-(1-x)=1 | C. | 1+(1-x)=x-3 | D. | 1-(1-x)=x-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
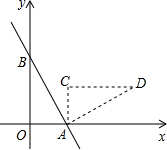 如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△ACD,则点D的坐标是(7,3).
如图,一次函数y=-$\frac{4}{3}$x+4的图象与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转90°后得到△ACD,则点D的坐标是(7,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com