
 S△ABC;
S△ABC;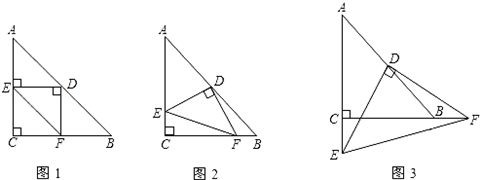
| 解:图2成立;图3不成立. 图2证明:过点D作DM⊥AC,DN⊥BC,则∠DME=∠DNF=∠MDN=90°, 又∵∠C=90°, ∴DM∥BC,DN∥AC, ∵D为AB边的中点, 由中位线定理可知:DN=  AC,MD= AC,MD= BC, BC,∵AC=BC, ∴MD=ND, ∵∠EDF=90°, ∴∠MDE+∠EDN=90°,∠NDF+∠EDN=90°, ∴∠MDE=∠NDF, ∴△DME≌△DNF, ∴S△DME=S△DNF, ∴S四边形DMCN=S四边形DECF=S△DEF+S△CEF, 由以上可知S四边形DMCN=  S△ABC, S△ABC,∴S△DEF+S△CEF=  S△ABC. S△ABC.图3不成立. 证明:△DEC≌△DBF(ASA,∠DCE=∠DBF=135°) S△DEF=S△DBF+S四边形DBFE, =S△DEC+S四边形DBFE, =S五边形DBFEC, =S△CFE+S△DBC, =S△CFE+ 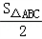 , ,∴S△DEF﹣S△CFE= 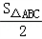 . .故S△DEF、S△CEF、S△ABC的关系是:S△DEF﹣S△CEF=  S△ABC. S△ABC. |
|


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
 如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( )
如图,已知Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AB边所在的直线为轴,将△ABC旋转一周,则所得几何体的表面积是( )A、
| ||
| B、24π | ||
C、
| ||
| D、12π |
查看答案和解析>>
科目:初中数学 来源: 题型:
 22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点.
22、如图所示,已知Rt△ABC中,AB=AC,BD平分∠ABC,CE⊥BD交BD延长线于E,BA、CE延长线相交于F点.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com