
【题目】如图,在平行四边形ABCD中,∠B、∠C的平分线交于P,且分别与AD交于E、F,
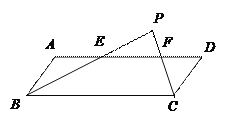
(1)求证:△BPC为直角三角形;
(2)若BC=16,CD=3,PE=8,求△PEF的面积.
【答案】(1)见解析;(2)24.
【解析】由平行四边形的性质得∠ABC+∠BCD=180°,由角平分线的定义可得∠PBC+∠BCP=90°,再根据三角形内角和可求∠BPC=90°;
(2)先根据等角对等边说明AB=AE=3,CD=DF=3,从而可求EF=10,根据勾股定理求出PF的长,然后根据三角形的面积公式计算即可.
(1)证明:∵四边形ABCD为平行四边形,
∴∠ABC+∠BCD=180°,
∵∠B、∠C的平分线交于P,
∴∠PBC+∠BCP=![]() (∠ABC+∠BCD )=90°
(∠ABC+∠BCD )=90°
∴∠BPC=90°,即△BPC为直角三角形;
(2)由题意可知,∠ABE=∠CBE=∠BEA,∠DCF=∠CBF=∠CFD,
∴AB=AE=3,CD=DF=3,
∴EF=10,
∴Rt△REF中,PE=8 ,EF=10,
∴PF=6,
∴△PEF的面积=24


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁. (Ⅰ)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至AC′的位置时,AC′的长为 ![]() m;
m;
(Ⅱ)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°,已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别为AB、CD上的点,且AE=CF= ![]() AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有条.
AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有条. 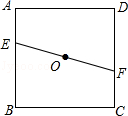
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D是线段AB上两点,已知AC:CD:DB=1:2:3,M、N分别为AC、DB的中点,且AB=12cm,
(1)求线段CD的长;
(2)求线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市自来水收费实行阶梯水价,收费标准如下表所示:
月用水量 | 不超过12吨的部分 | 超过12吨的部分且 不超过18吨的部分 | 超过18吨的部分 |
收费标准 | 2元/吨 | 2.5元/吨 | 3元/吨 |
(1)某用户四月份用水量为16吨,需交水费为多少元?
(2)某用户五月份交水费50元,所用水量为多少吨?
(3)某用户六月份用水量为a吨,需要交水费为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某修理厂需要购进甲、乙两种配件,经调查,每个甲种配件的价格比每个乙种配件的价格少0.4万元,且用16万元购买的甲种配件的数量与用24万元购买的乙种配件的数量相同.
(1)求每个甲种配件、每个乙种配件的价格分别为多少万元;
(2)现投入资金80万元,根据维修需要预测,甲种配件要比乙种配件至少要多22件,问乙种配件最多可购买多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)填空:点B在数轴上表示的数是 ,点C在数轴上表示的数是 ;
(2)若线段CD以每秒3个单位的速度向右匀速运动,当点D运动到A时,线段CD与线段AB开始有重叠部分,此时线段CD运动了 秒;
(3)在(2)的条件下,线段CD继续向右运动,问再经过 秒后,线段CD与线段AB不再有重叠部分;
(4)若线段AB、CD同时从图中位置出发,线段AB以每秒2个单位的速度向左匀速运动,线段CD仍以每秒3个单位的速度向右匀速运动,点P是线段CD的中点,问运动几秒时,点P与线段AB两端点(A或B)的距离为1个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 若|a|=﹣a,则 a 一 定是负数
B. 单项式 x3y2z 的系数为 1,次数是 6
C. 若 AP=BP,则点 P 是线段 AB 的中点
D. 若∠AOC=![]() ∠AOB,则射线 OC 是∠AOB 的平分线
∠AOB,则射线 OC 是∠AOB 的平分线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com