
【题目】解方程组:
(1)![]()
(2)![]()
(3)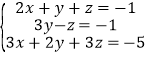
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)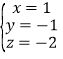 .
.
【解析】
1)根据解方程的方法可以解答此方程;
(2)根据加减消元法可以解答此方程;
(3)根据解三元一次方程组的方法可以解答此方程.
解:(1)![]() +1=
+1=![]()
去分母,得
3(4x﹣1)+12=4(2x+3)
去括号,得
12x﹣3+12=8x+12
移项及合并同类项,得
4x=3
系数化为1,得
x=![]() ;
;
(2)![]()
①×3+②,得
16x=48
解得,x=3,
将x=3代入①,得
y=2
故原方程组的解是![]() ;
;
(3)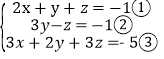
①+②,得
2x+4y=﹣2④
②×3+③,得
3x+11y=﹣8⑤
④×3﹣⑤×2,得
﹣10y=10
解得,y=﹣1,
将y=﹣1代入④,得
x=1,
将x=1,y=﹣1代入①,得
z=﹣2
故原方程组的解是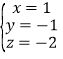 .
.


科目:初中数学 来源: 题型:
【题目】某中学计划从一文体公司购买甲,乙两种型号的小黑板,经洽谈,购买一块甲型小黑板比购买一块乙型小黑板多用20元,且购买2块甲型小黑板和3块乙型小黑板共需440元.
(1)求购买一块甲型小黑板、一块乙型小黑板各需多少元?
(2)根据该中学实际情况,需从文体公司购买甲,乙两种型号的小黑板共60块,要求购买甲,乙两种型号小黑板的总费用不超过5240元.并且购买甲型小黑板的数量不小于购买乙型小黑板数量的 ![]() .则该中学从文体公司购买甲,乙两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
.则该中学从文体公司购买甲,乙两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天的早晨,小明骑自行车从家出发,到离家1050米的书店买书,出发1分钟后,他到达离家150米的地方,又过1分钟后,小明加快了速度.如图所示是小明从家出发后离家的路程y(米)与他骑自行车的时间x(分钟)之间的函数图象.根据图象解答下列问题: 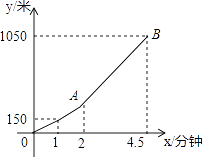
(1)直接写出点A的坐标,并求线段AB所在的直线的函数解析式.
(2)求小明出发多长时间后,离书店还剩210米的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,垂直于地面的灯柱AB被一钢缆CD固定,CD与地面成45°夹角(∠CDB=45°);为了使灯柱更牢固,在C点上方2米处再新加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),求线段ED的长.(结果精确到0.1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33) 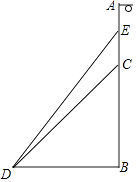
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC于点E. 
(1)求证:AC⊥BD;
(2)若AB=14,cos∠CAB= ![]() ,求线段OE的长.
,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
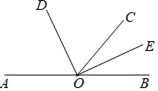
如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.求∠DOE的度数.
解:因为OD是∠AOC的平分线,
所以∠COD=![]() ∠AOC.
∠AOC.
因为OE是∠BOC 的平分线,
所以 =![]() ∠BOC.
∠BOC.
所以∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠B、∠C的平分线交于P,且分别与AD交于E、F,
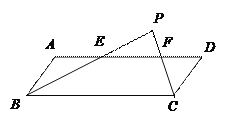
(1)求证:△BPC为直角三角形;
(2)若BC=16,CD=3,PE=8,求△PEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com