
【题目】某中学计划从一文体公司购买甲,乙两种型号的小黑板,经洽谈,购买一块甲型小黑板比购买一块乙型小黑板多用20元,且购买2块甲型小黑板和3块乙型小黑板共需440元.
(1)求购买一块甲型小黑板、一块乙型小黑板各需多少元?
(2)根据该中学实际情况,需从文体公司购买甲,乙两种型号的小黑板共60块,要求购买甲,乙两种型号小黑板的总费用不超过5240元.并且购买甲型小黑板的数量不小于购买乙型小黑板数量的 ![]() .则该中学从文体公司购买甲,乙两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
.则该中学从文体公司购买甲,乙两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
【答案】
(1)解:购买一块甲型小黑板需x元、一块乙型小黑板需y元,
根据题意得: ![]() ,
,
解得: ![]()
(2)解:设购买a块甲型小黑板,则购买(60﹣a)块乙型小黑板,
根据题意得: 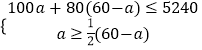 ,
,
解得:20≤a≤22,
∴当a=20时,60﹣a=40;当a=21时,60﹣a=39;当a=22时,60﹣a=38.
∴方案一:购买20块甲型小黑板、40块乙型小黑板;方案二:购买21块甲型小黑板、39块乙型小黑板;方案三:购买22块甲型小黑板、38块乙型小黑板.
∵100>80,
∴购买的甲型小黑板越少总费用越低,
∴方案一总费用最低
【解析】(1)购买一块甲型小黑板需x元、一块乙型小黑板需y元,根据两种小黑标费用间的关系,即可得出关于x、y的二元一次方程组,解之即可得出结论;(2)设购买a块甲型小黑板,则购买(60﹣a)块乙型小黑板,根据总费用不超过5240元且购买甲型小黑板的数量不小于购买乙型小黑板数量的 ![]() ,即可得出关于a的一元一次不等式组,解之即可得出a的取值范围,从而即可得出各购买方案,再根据两种小黑板单价间的关系,即可得出总费用最低的购买方案.
,即可得出关于a的一元一次不等式组,解之即可得出a的取值范围,从而即可得出各购买方案,再根据两种小黑板单价间的关系,即可得出总费用最低的购买方案.
【考点精析】本题主要考查了一元一次不等式组的应用的相关知识点,需要掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能正确解答此题.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
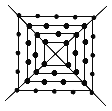
【题目】如图,有一个形如四边形的点阵,第1层每边有2个点,第2层每边有3个点,第3层每边有4个点,依此类推.
(1)第10层共有 个点,第n层共有 个点;
(2)如果某一层共有96个点,它是第几层?
(3)有没有一层点数为150个点,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF⊥AG于点F,DE⊥AG于点E,探究BF,DE,EF之间的数量关系,第一学习小组合作探究后,得到DE﹣BF=EF,请证明这个结论; 
(2)若(1)中的点G在CB的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时BF,DE,EF之间的数量关系; 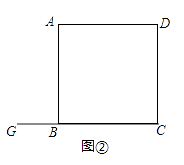
(3)如图③,四边形ABCD内接于⊙O,AB=AD,E,F是AC上的两点,且满足∠AED=∠BFA=∠BCD,试判断AC,DE,BF之间的数量关系,并说明理由 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
(1) 点B的坐标为__________,不等式![]() 的解集为___________
的解集为___________
(2) 若S△COE=S△ADE,求点D的坐标;
(3) 如图2,以CD为边作菱形CDFG,且∠CDF=60°.当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△AEC=S△ABC,其中正确结论有( )个.
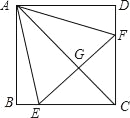
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁. (Ⅰ)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至AC′的位置时,AC′的长为 ![]() m;
m;
(Ⅱ)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°,已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com