
【题目】填空,完成下列说理过程
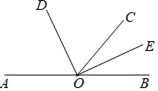
如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.求∠DOE的度数.
解:因为OD是∠AOC的平分线,
所以∠COD=![]() ∠AOC.
∠AOC.
因为OE是∠BOC 的平分线,
所以 =![]() ∠BOC.
∠BOC.
所以∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
(1) 点B的坐标为__________,不等式![]() 的解集为___________
的解集为___________
(2) 若S△COE=S△ADE,求点D的坐标;
(3) 如图2,以CD为边作菱形CDFG,且∠CDF=60°.当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)如图,直线l1的解析表达式为:![]() ,且l1与x轴
,且l1与x轴
交于点D,直线l2经过点A,B,直线l1,l2交于点C.
【1】(1)求直线l2的函数关系式;
【2】(2)求△ADC的面积;
【3】(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.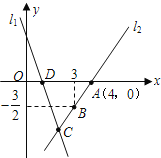
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P,点Q分别代表两个村庄,直线l代表两个村庄中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站.
(1)若考虑到村庄P居住的老年人较多,计划建一个离村庄P最近的车站,请在公路l上画出车站的位置(用点M表示),依据是 ;
(2)若考虑到修路的费用问题,希望车站的位置到村庄P和村庄Q的距离之和最小,请在公路l上画出车站的位置(用点N表示),依据是 .
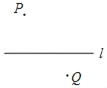
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁. (Ⅰ)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至AC′的位置时,AC′的长为 ![]() m;
m;
(Ⅱ)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°,已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别为AB、CD上的点,且AE=CF= ![]() AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有条.
AB,点O为线段EF的中点,过点O作直线与正方形的一组对边分别交于P、Q两点,并且满足PQ=EF,则这样的直线PQ(不同于EF)有条. 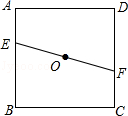
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)填空:点B在数轴上表示的数是 ,点C在数轴上表示的数是 ;
(2)若线段CD以每秒3个单位的速度向右匀速运动,当点D运动到A时,线段CD与线段AB开始有重叠部分,此时线段CD运动了 秒;
(3)在(2)的条件下,线段CD继续向右运动,问再经过 秒后,线段CD与线段AB不再有重叠部分;
(4)若线段AB、CD同时从图中位置出发,线段AB以每秒2个单位的速度向左匀速运动,线段CD仍以每秒3个单位的速度向右匀速运动,点P是线段CD的中点,问运动几秒时,点P与线段AB两端点(A或B)的距离为1个单位?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com