
【题目】(本题满分12分)如图,直线l1的解析表达式为:![]() ,且l1与x轴
,且l1与x轴
交于点D,直线l2经过点A,B,直线l1,l2交于点C.
【1】(1)求直线l2的函数关系式;
【2】(2)求△ADC的面积;
【3】(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.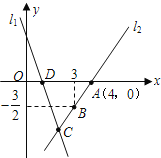
【答案】
【1】设直线![]() 的函数关系式为y=kx+b
的函数关系式为y=kx+b
∵当x=4时,y=0;当x=3时,y=![]() ,
,
∴ ,∴
,∴
∴直线l2的函数关系式为![]() .
.
【2】由y=3x+3,令y=0,得3x+3=0,
∴x=1,
∴D(1,0);
由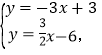
解得![]()
∴C(2,3),
∵AD=3,
∴![]()
【3】如图所示:存在;
A(4,0),C(2,3),D(1,0),
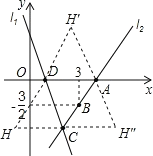
若以CD为对角线,
则CH=AD=3,
∴点H的坐标为:(1,3);
若以AC为对角线,
则CH′=AD=3,
∴点H′(5,3);
若以AD为对角线,
可得H″(3,3);
∴点H的坐标为:(3,3)(5,3)(1,3).
【解析】(1)结合图形可知点![]() 和点A在坐标,故设
和点A在坐标,故设![]() 的解析式为
的解析式为![]() ,由图联立方程组求出
,由图联立方程组求出![]() 的值;
的值;
(2)已知![]() 的解析式,令
的解析式,令![]() 求出x的值即可得出点D在坐标;联立两直线方程组,求出交点C的坐标,进而可求出
求出x的值即可得出点D在坐标;联立两直线方程组,求出交点C的坐标,进而可求出![]()
(3)存在;根据平行四边形的性质,可知一定存在3个这样的点,规律为H、C坐标之和等于A、D坐标之和,设出代入即可得出H的坐标.
(1)设直线![]() 的解析表达式为y=kx+b,
的解析表达式为y=kx+b,
由图象知:x=4,y=0;
x=3,![]()
∴∴ ,∴
,∴
∴直线l2的解析表达式为![]() .
.
(2)由y=3x+3,令y=0,得3x+3=0,
∴x=1,
∴D(1,0);
由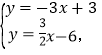
解得![]()
∴C(2,3),
∵AD=3,
∴![]()
![]() 如图所示:存在;
如图所示:存在;
A(4,0),C(2,3),D(1,0),

若以CD为对角线,
则CH=AD=3,
∴点H的坐标为:(1,3);
若以AC为对角线,
则CH′=AD=3,
∴点H′(5,3);
若以AD为对角线,
可得H″(3,3);
∴点H的坐标为:(3,3)(5,3)(1,3).


科目:初中数学 来源: 题型:
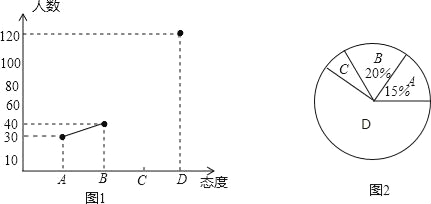
【题目】中学生带手机上学的现象越来越受到社会的关注,为此某记者随机调查了市区某校七年级若干名中学生家长对这种现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).统计员在将测试数据绘制成图表时发现,反对漏统计6人,赞成漏统计4人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
家长对中学生带手机上学各项态度人数统计表和统计图:
态度 | 调整前人数 | 调整后人数 |
A.无所谓 | 30 | 30 |
B.基本赞成 | 40 | 40 |
C.赞成 | ||
D.反对 | 114 | 120 |
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)填写统计表,并根据调整后数据补全折线统计图;
(3)根据抽样调查结果,请你估计该市城区6000名中学生家长中有多少名家长持反对态度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,垂直于地面的灯柱AB被一钢缆CD固定,CD与地面成45°夹角(∠CDB=45°);为了使灯柱更牢固,在C点上方2米处再新加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),求线段ED的长.(结果精确到0.1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33) 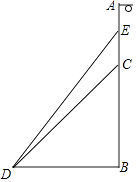
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.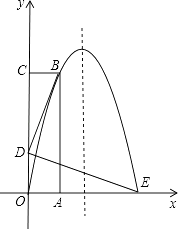
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
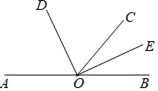
如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.求∠DOE的度数.
解:因为OD是∠AOC的平分线,
所以∠COD=![]() ∠AOC.
∠AOC.
因为OE是∠BOC 的平分线,
所以 =![]() ∠BOC.
∠BOC.
所以∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
某校七年级共有10个班,320名同学,地理老师为了了解全年级同学明年选考时,选修地理学科的意向,请小丽,小明,小东三位同学分别进行抽样调查.三位同学调查结果反馈如图:

(1)小丽、小明和小东三人中,你认为哪位同学的调查结果较好地反映了该校七年级同学选修地理的意向,请说出理由.
(2)估计全年级有意向选修地理的同学的人数为 人,理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为1的网格中,等腰直角三角形ACB与ECD的顶点都在网格点上,点N、M分别为线段AB、DE上的动点,且BN=EM. (Ⅰ)如图①,当BN= ![]() 时,计算CN+CM的值等于
时,计算CN+CM的值等于 ![]()
(Ⅱ)当CN+CM取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段CN和CM,并简要说明点M和点N的位置是如何找到的(不要求证明).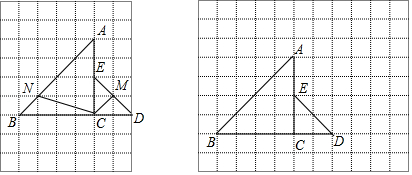
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABOC中,∠A=60°,它的一个顶点C在反比例函数y= ![]() 的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )
的图象上,若将菱形向下平移2个单位,点A恰好落在函数图象上,则反比例函数解析式为( )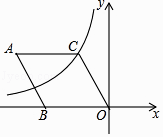
A.y=﹣ ![]()
B.y=﹣ ![]()
C.y=﹣ ![]()
D.y= ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com