
【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.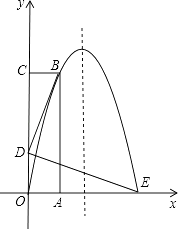
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标.
【答案】
(1)
解:将点B(1,4),E(3,0)的坐标代入抛物线的解析式得: ![]() ,
,
解得: ![]() ,
,
抛物线的解析式为y=﹣2x2+6x
(2)
解:如图1所示;
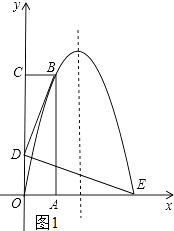
∵BD⊥DE,
∴∠BDE=90°.
∴∠BDC+∠EDO=90°.
又∵∠ODE+∠DEO=90°,
∴∠BDC=∠DE0.
在△BDC和△DOE中, 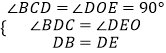 ,
,
∴△BDC≌△DEO(AAS).
∴OD=AO=1.
∴D(0,1)
(3)
解:如图2所示:作点B关于抛物线的对称轴的对称点B′,连接B′D交抛物线的对称轴与点M.

∵x=﹣ ![]() =
= ![]() ,
,
∴点B′的坐标为(2,4).
∵点B与点B′关于x= ![]() 对称,
对称,
∴MB=B′M.
∴DM+MB=DM+MB′.
∴当点D、M、B′在一条直线上时,MD+MB有最小值(即△BMD的周长有最小值).
∵由两点间的距离公式可知:BD= ![]() =
= ![]() ,DB′=
,DB′= ![]() =
= ![]() ,
,
∴△BDM的最小值= ![]() +
+ ![]() .
.
设直线B′D的解析式为y=kx+b.
将点D、B′的坐标代入得: ![]() ,
,
解得: ![]() ,
,
∴直线DB′的解析式为y= ![]() x+1.
x+1.
将x= ![]() 代入得:y=
代入得:y= ![]() .
.
∴M( ![]() ,
, ![]() )
)
【解析】(1)将点B(1,4),E(3,0)的坐标代入抛物线的解析式,得到关于a、b的方程组,求得a、b的值,从而可得到抛物线的解析式;(2)依据同角的余角相等证明∠BDC=∠DE0,然后再依据AAS证明△BDC≌△DEO,从而得到OD=AO=1,于是可求得点D的坐标;(3)作点B关于抛物线的对称轴的对称点B′,连接B′D交抛物线的对称轴与点M.先求得抛物线的对称轴方程,从而得到点B′的坐标,由轴对称的性质可知当点D、M、B′在一条直线上时,△BMD的周长有最小值,依据两点间的距离公式求得BD和B′D的长度,从而得到三角形的周长最小值,然后依据待定系数法求得D、B′的解析式,然后将点M的横坐标代入可求得点M的纵坐标.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
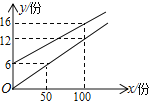
【题目】武汉市某校实行学案式教学,需印制若干份数学学案.印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示
(1) 求甲、乙两种收费方式的函数关系式;
(2) 当印刷多少份学案时,两种印刷方式收费一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地。假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等,)又顺水航行返回万州,若该轮船从万州出发后所用时间为x(小时),轮船距万州的距离为y(千米),则下列各图中,能反映y与x之间函数关系的图象大致是【 】
A.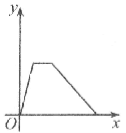 B.
B.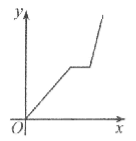 C.
C.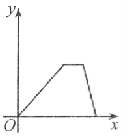 D.
D.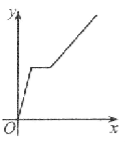
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学现要从两位男生和两位女生中,选派两位同学分别作为1号选手和2号选手代表学校参加汉字听写大赛.
(1)请用树形图或列表法列举出所有可能选派的结果;
(2)求恰好选派一男一女两位同学参赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD. 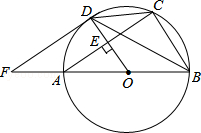
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)如图,直线l1的解析表达式为:![]() ,且l1与x轴
,且l1与x轴
交于点D,直线l2经过点A,B,直线l1,l2交于点C.
【1】(1)求直线l2的函数关系式;
【2】(2)求△ADC的面积;
【3】(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、D、C、H为顶点的四边形是平行四边形?若存在,请直接写出点H的坐标;若不存在,请说明理由.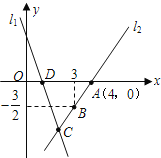
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是假命题的是( )
A. 在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
B. 在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形
C. 在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形
D. 在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长方形纸片按如图所示的方式折叠,BC、BD为折痕.若∠ABC=25°,则∠DBE的度数为( )
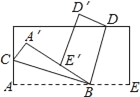
A. 50° B. 65° C. 45° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com