
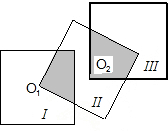
 有若干个边长都为2的小正方形.若小正方形Ⅱ的一个顶点在小正方形I的中心O1,如图所示;类似地小正方形Ⅲ的一个顶点在小正方形Ⅱ的中心O2,并且小正方形I与小正方形Ⅲ不相重叠,如果若干个小正方形都按这种方法拼接,问需要几个小正方形能使拼接出的图形的阴影部分的面积等于一个小正方形的面积,并给出你的证明过程.
有若干个边长都为2的小正方形.若小正方形Ⅱ的一个顶点在小正方形I的中心O1,如图所示;类似地小正方形Ⅲ的一个顶点在小正方形Ⅱ的中心O2,并且小正方形I与小正方形Ⅲ不相重叠,如果若干个小正方形都按这种方法拼接,问需要几个小正方形能使拼接出的图形的阴影部分的面积等于一个小正方形的面积,并给出你的证明过程.| 1 |
| 4 |
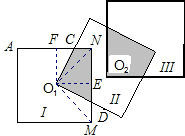 需要5个小正方形能使拼接出的图形的阴影部分面积等于一个小正方形的面积.理由如下:
需要5个小正方形能使拼接出的图形的阴影部分面积等于一个小正方形的面积.理由如下:| 1 |
| 4 |
|
| 1 |
| 4 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:北京市海淀区2007-2008学年度九年级第一学期期中练习数学试题 题型:059
有若干个边长都为2的小正方形.若小正方形II的一个顶点在小正方形I的中心O1,如图所示;类似地小正方形III的一个顶点在小正方形II的中心O2,并且小正方形I与小正方形III不相重叠,如果若干个小正方形都按这种方法拼接,问需要几个小正方形能使拼接出的图形的阴影部分的面积等于一个小正方形的面积,并给出你的证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
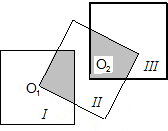 有若干个边长都为2的小正方形.若小正方形Ⅱ的一个顶点在小正方形I的中心O1,如图所示;类似地小正方形Ⅲ的一个顶点在小正方形Ⅱ的中心O2,并且小正方形I与小正方形Ⅲ不相重叠,如果若干个小正方形都按这种方法拼接,问需要几个小正方形能使拼接出的图形的阴影部分的面积等于一个小正方形的面积,并给出你的证明过程.
有若干个边长都为2的小正方形.若小正方形Ⅱ的一个顶点在小正方形I的中心O1,如图所示;类似地小正方形Ⅲ的一个顶点在小正方形Ⅱ的中心O2,并且小正方形I与小正方形Ⅲ不相重叠,如果若干个小正方形都按这种方法拼接,问需要几个小正方形能使拼接出的图形的阴影部分的面积等于一个小正方形的面积,并给出你的证明过程.查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市师大三附中九年级(上)期中数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2007-2008学年北京市海淀区九年级(上)期中数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com